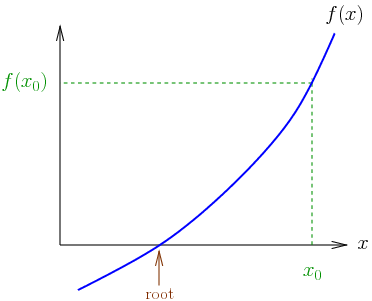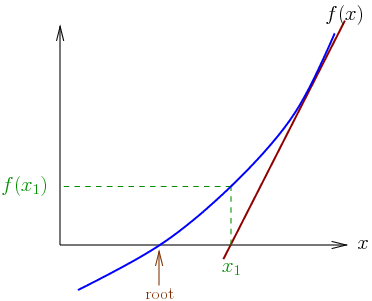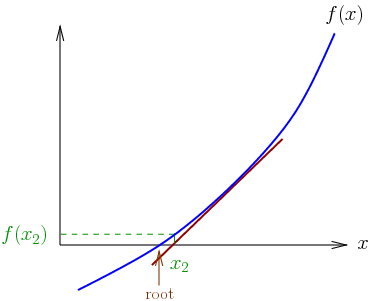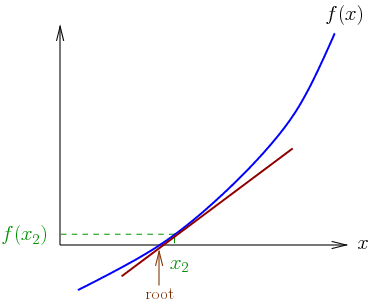
Sayısal çözümlemede, Isaac Newton ve Joseph Raphson‘dan ismini alan Newton – Raphson yöntemi (Newton yöntemi olarak da bilinir), gerçek değerli işlevlerin kökleri için art arda ve hızlı bir şekilde daha iyi yaklaşımlar bulmak için kullanılan bir yöntemdir. Newton-Raphson yöntemi, denklemleri sayısal olarak çözmek için güçlü bir tekniktir. Sürekli ve farklılaşabilir bir fonksiyonun ona teğet düz bir çizgi ile yaklaşabileceği fikrini kullanır. Fikir, gerçek köke makul bir şekilde yakın olan bir başlangıç tahmini ile başlar, daha sonra işlevi teğet çizgisiyle yaklaşıklaştırmak ve bu teğet çizginin x kesişimini temel cebir işlemi ile hesaplamak. Bu x kesme noktası orijinal fonksiyonun köküne ilk tahminden daha iyi bir yaklaşım olacaktır ve yöntem tekrarlanabilir. Yöntem, gerçek…
-
-
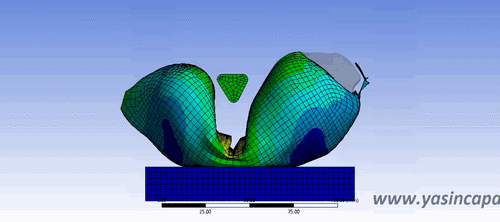
Sonlu Elemanlar Yöntemde Doğrusal Olmama Durumu (Nonlinearities in FEM)
Doğrusal (Linear) bir FEA çalışması, gerçek koşulları sadece bir dizi kısıtlayıcı koşul tanımlandığında simüle eder. Bunlar, tüm sapmaların çok küçük olduğunu ve yüklerin neden olduğu stress ve strain doğrusal ilişkilerinin (Hooke yasası) korunmasına izin verecek kadar küçük kalmasını içerir. Doğrusal bir analiz, geometrinin kararsız bölgelerini tespit edemediği için hedefi kaçırabilir. Bu bölgelerde yük genliğindeki küçük bir değişiklik bile önemli ölçüde farklı deformasyonlara yol açabilir. Lineer sonlu elemanlar yöntemi birçok şeyi basitleştirir. Örneğin, malzeme asla kopmayacak ve sonuç olarak modelde gerçekçi olmayan yüksek gerilimler meydana gelecektir. Ayrıca, doğrusal olmayan geometri dikkate alınmadığından başarısızlığı tahmin edemeyebilirsiniz. FEA (Sonlu Elemanlar Analizi), FEM (Sonlu Elemanlar Yöntemi) adı verilen sayısal bir teknik kullanılarak herhangi bir…