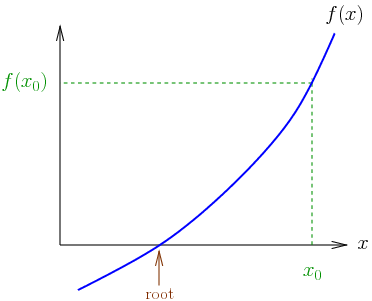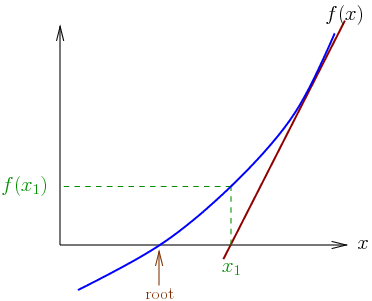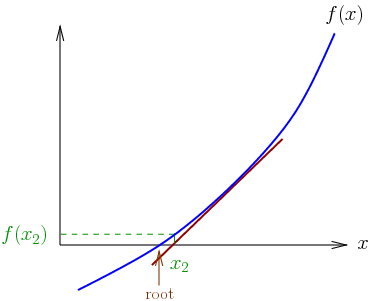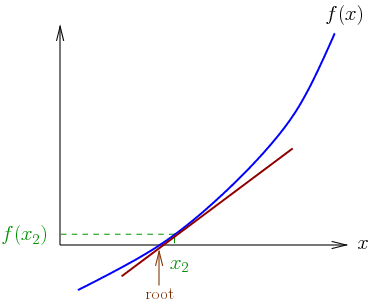
Sayısal çözümlemede, Isaac Newton ve Joseph Raphson‘dan ismini alan Newton – Raphson yöntemi (Newton yöntemi olarak da bilinir), gerçek değerli işlevlerin kökleri için art arda ve hızlı bir şekilde daha iyi yaklaşımlar bulmak için kullanılan bir yöntemdir.
Newton-Raphson yöntemi, denklemleri sayısal olarak çözmek için güçlü bir tekniktir. Sürekli ve farklılaşabilir bir fonksiyonun ona teğet düz bir çizgi ile yaklaşabileceği fikrini kullanır.
Fikir, gerçek köke makul bir şekilde yakın olan bir başlangıç tahmini ile başlar, daha sonra işlevi teğet çizgisiyle yaklaşıklaştırmak ve bu teğet çizginin x kesişimini temel cebir işlemi ile hesaplamak. Bu x kesme noktası orijinal fonksiyonun köküne ilk tahminden daha iyi bir yaklaşım olacaktır ve yöntem tekrarlanabilir.

Yöntem, gerçek sayılar x üzerinde tanımlanmış bir fonksiyon f, fonksiyonunun türevi f ′ ve f fonksiyonunun bir kökü için ilk tahmin x0 ile başlar. İşlev yeterli varsayımları karşılıyorsa ve ilk tahmin yakınsa, daha iyi bir yaklaşık x1;
Kök x0’dan daha iyi bir yaklaşım vardır. Geometrik olarak, (x1, 0), x-ekseninin kesişimidir ve f grafiğinin (x0, f (x0)) ‘da teğetidir. Geliştirilmiş tahmin, başlangıç noktasındaki doğrusal yaklaşımın eşsiz köküdür. İşlem, yeterince doğru bir değere ulaşılana kadar tekrarlanır.
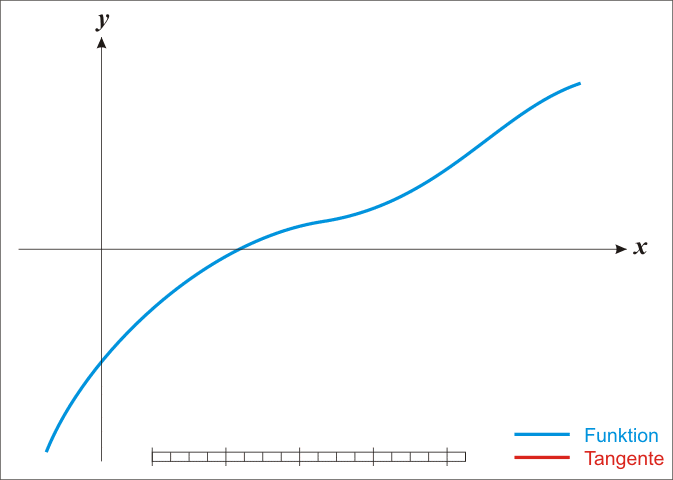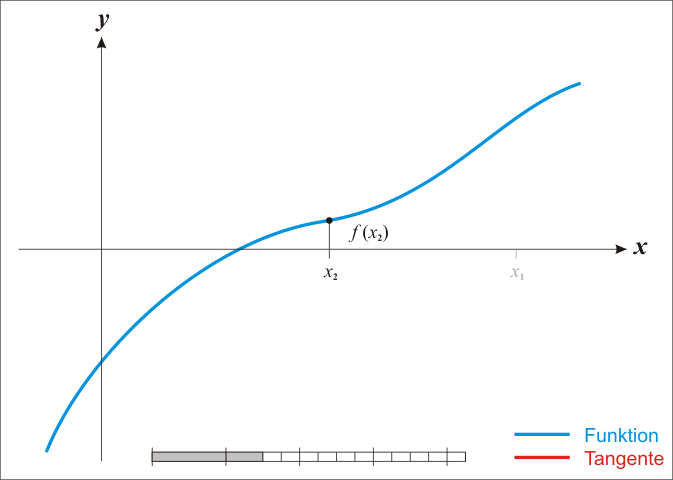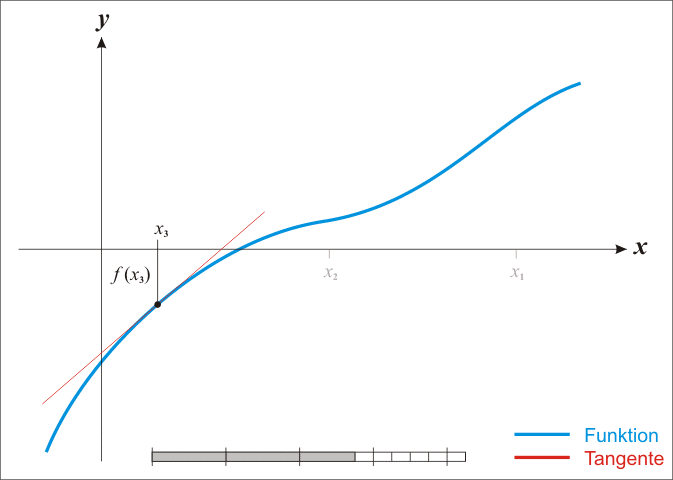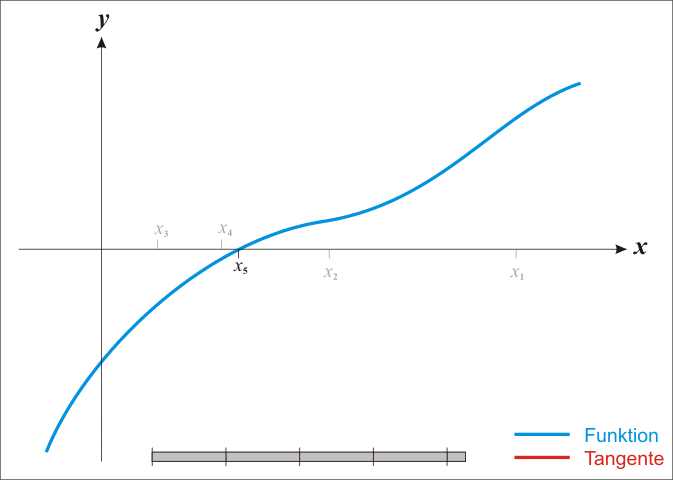
Bu yöntemde yaklaşımlardan birinin, gerçek köke makul bir şekilde yakın olan bir ilk tahminle başladığını, daha sonra fonksiyonun teğet çizgisiyle yaklaştığını ve birinin bu teğet çizginin x-kesişimini hesapladığını takip eder. Yöntem ayrıca karmaşık fonksiyonlara ve denklem sistemlerine de genişletilebilir.
Genel olarak, yakınsama ikinci dereceden; yöntem kök üzerinde yakınsak olduğu için, kök ve yaklaşık değer arasındaki fark her adımda karelerdir.
Ayrıca yöntemle ilgili bazı zorluklar vardır; Newton yönteminin ikinci dereceden yakınsamasının kanıtında yapılan varsayımlar karşılanmazsa, çokluğun kökleri için yakınsama yavaşlar.
Formülasyonun Temeli
Newton-Raphson yöntemi, bir işlevin Taylor serisinin ilk birkaç terimini kullanan bir kök bulma algoritmasıdır. F(x) = 0 denklemini çözmek için önce, f(x) fonksiyonunun Taylor genleşmesi dikkate alınır,
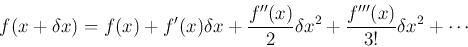
f(x) linear (doğrusal) ise, yalnızca ilk iki terim olan sabit ve doğrusal terimler sıfırdan farklıdır,
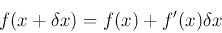
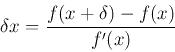
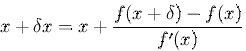

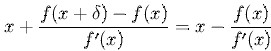
f(x) nonlinear (doğrusal olmayan) ise, Xn+1, önceki yaklaşık Xn’ye dayalı olarak kökün geliştirilmiş bir yaklaşımdır, köke bu yineleme ile yaklaşılır,
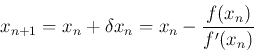
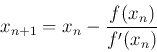
Örnek Olarak
(2x^3)-2x-1= 0 denklemini çözelim. Bu durumda f(x) = (2x^3)-2x-1, yani f′(x) = (6x^2)-2.
Formül,
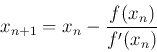
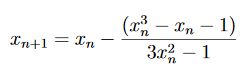
Bu sorun için uygun bir ilk tahmin x0’a karar vermemiz gerekiyor. F(1) = – 1 <0 ve f(2) = 11> 0. Bu nedenle, 1 ve 2 arasında f (x) = 0 kökü bulunmalıdır. İlk tahminimiz olarak x0 = 1’i alalım. Sonrasında,
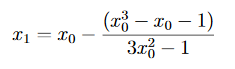
x0 = 1 ile, x1= 1.25 değeri bulunur.
Devem edersek,
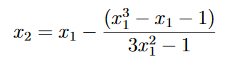
x1 = 1.25 ile, x2 = 1.1949 değeri bulunur.
Bir sonraki adım,
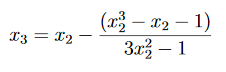
x3 = 1.1915. Devam edicek olursak, bulunacak değerler; x4=1.191487884, x5=1.191487883, vb.
İstenilen yakınsama derecesine ulaştığımızda durabiliriz. Kökün 1.191487883 olduğu sonucuna varıyoruz.
Özetlersek
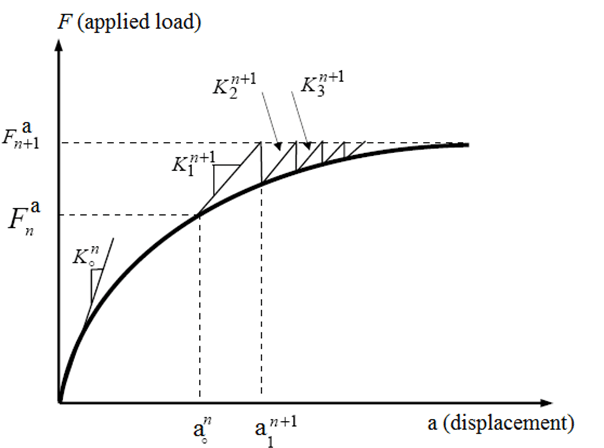
- Doğrusal olmayan bir yapı, düzeltmelerle tekrarlanan bir dizi doğrusal yaklaşım kullanılarak analiz edilebilir.
- Bazı FEA yazılımları Newton-Raphson Yöntemi adı verilen yinelemeli bir işlem kullanır. Her yineleme bir denge yinelemesi olarak bilinir.
- Doğrusal olmayan analizde, yük ve yer değiştirme arasındaki ilişki, başlangıçtaki sertliğe bağlı olarak tek bir çözümle belirlenemez.
- Artık kuvvetler kabul edilebilir bir tolerans dahilinde ise, çözüm yakınsamıştır.
- Artık kuvvetler kabul edilebilir bir tolerans dahilinde değilse, çözüm yakınsamaz, bu nedenle yeni bir hedef sertlik matrisi tanımlanır ve işlem tekrarlanır.
Denge yinelemesi (Equilibrium iteration):
Doğrusal olmayan çözümde, denge yinelemeleri Newton-Raphson yöntemi kullanılarak yakınsama için gerekli düzeltici çözümlerdir.
Halley’s motodu, detaylı olarak ilerleyen makalelerde değinilecektir.
Kaynaklar:
wikipedia.org
sciencedirect.com
personal.maths.surrey.ac.uk