Taylor expansion matematikteki en yararlı fikirlerden biridir. Çoğu fonksiyon ve polinomun çözümü genellikle düzgündür. Polinomların çalışması, hemen hemen tüm diğer fonksiyon türlerinden daha kolaydır, ayrıca polinomlar büyük ölçüde fonksiyonlara yaklaşabilir. Taylor formülü bize f ‘in hemen hemen her düzgün fonksiyonu için polinom genişlemesi için bir denklem verir.
Taylor Serisi
Taylor serisi, matematikte bir fonksiyonun tek bir noktada, fonksiyonun türevleri cinsinden ifade edilen sonsuz bir terim toplamıdır. En yaygın fonksiyonlar için Taylor serisinin fonksiyonu ve toplamı, bu noktanın yakınına eşittir. Taylor serisi adını 1715’te seriyi tanıtan Brook Taylor’dan almıştır.
Taylor Teorisi
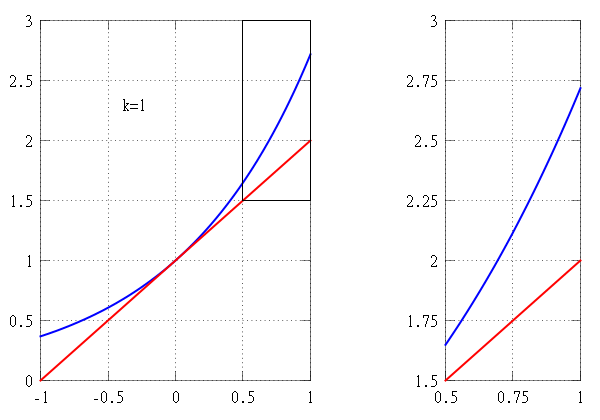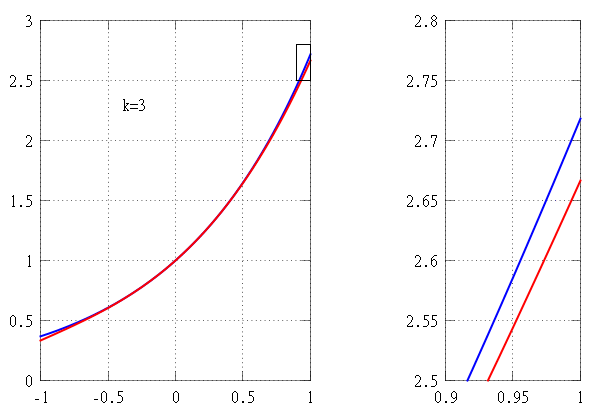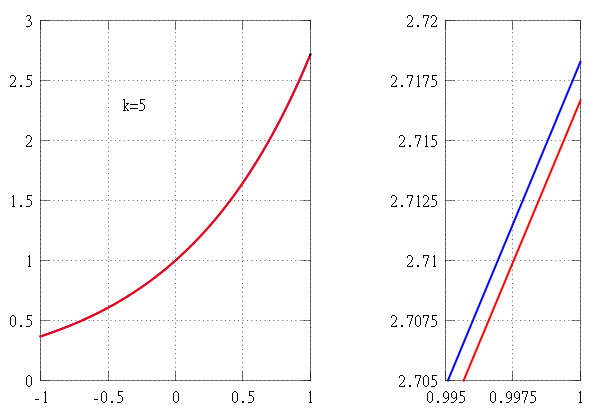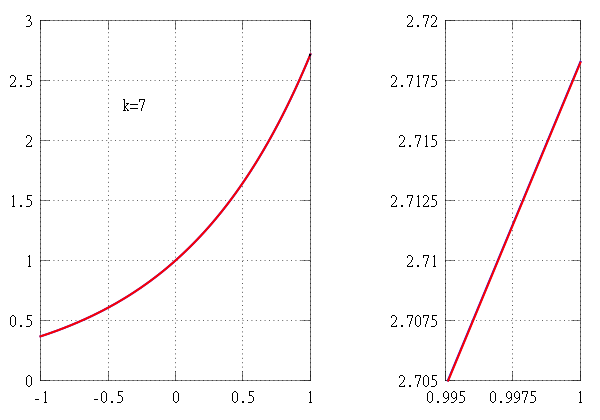
Hesaplamada Taylor teoremi, k ‘ınci sıra Taylor polinomu olarak adlandırılan k dereceli bir polinom tarafından verilen bir nokta etrafında k-defa türevlenebilir bir fonksiyonun yaklaşıklığını verir. Düzgün bir fonksiyon için, Taylor polinomu fonksiyonun Taylor serisinin k mertebesinde kesilmesidir. Birinci dereceden Taylor polinomu, fonksiyonun doğrusal yaklaşımıdır ve ikinci dereceden Taylor polinomu genellikle ikinci dereceden yaklaşım olarak adlandırılır. Taylor teoreminin birkaç versiyonu vardır ve bazıları Taylor polinomu ile fonksiyonun yaklaşıklık hatası hakkında açık tahminler verir.
Taylor teoremi, üstel fonksiyon ve trigonometrik fonksiyonlar gibi birçok transandantal fonksiyonun değerlerini doğru bir şekilde hesaplamak için basit aritmetik formüller verir. Analitik fonksiyonların çalışmasının başlangıç noktasıdır ve matematiğin çeşitli alanlarında, ayrıca sayısal analiz ve matematiksel fizikte temeldir.
Bir Taylor serisinin ilk n + 1 terimlerinin oluşturduğu kısmi toplam, fonksiyonun n inci Taylor polinomu olarak adlandırılan n dereceli bir polinomdur. Taylor polinomları, n arttıkça genellikle daha iyi hale gelen bir fonksiyonun yaklaşık değerleridir.
Taylor Serisi vs Taylor Teorisi
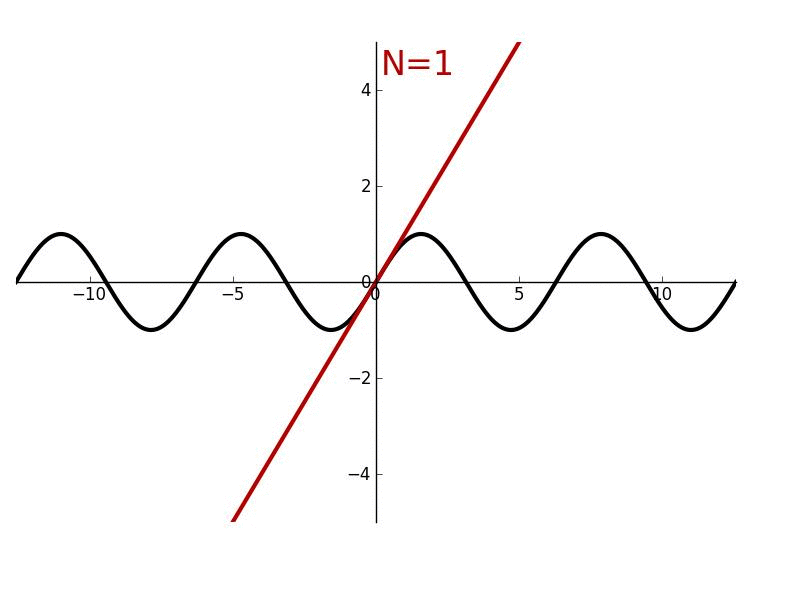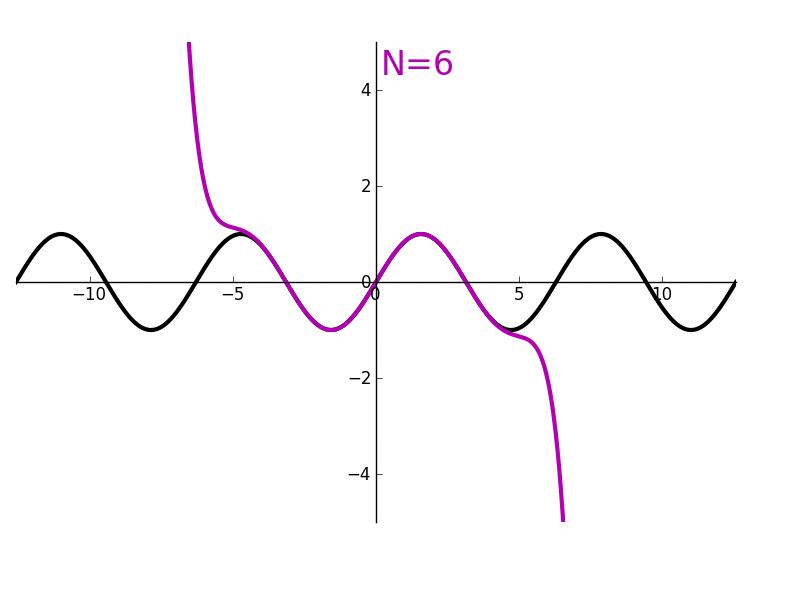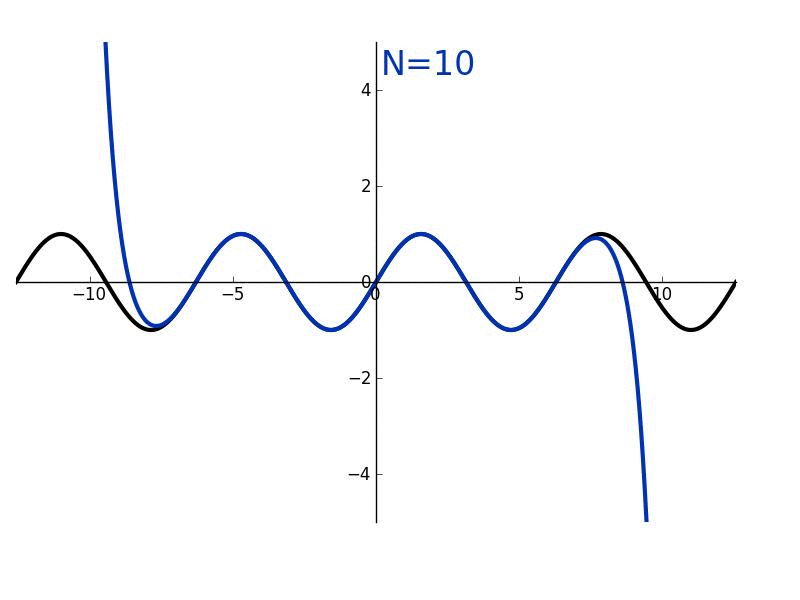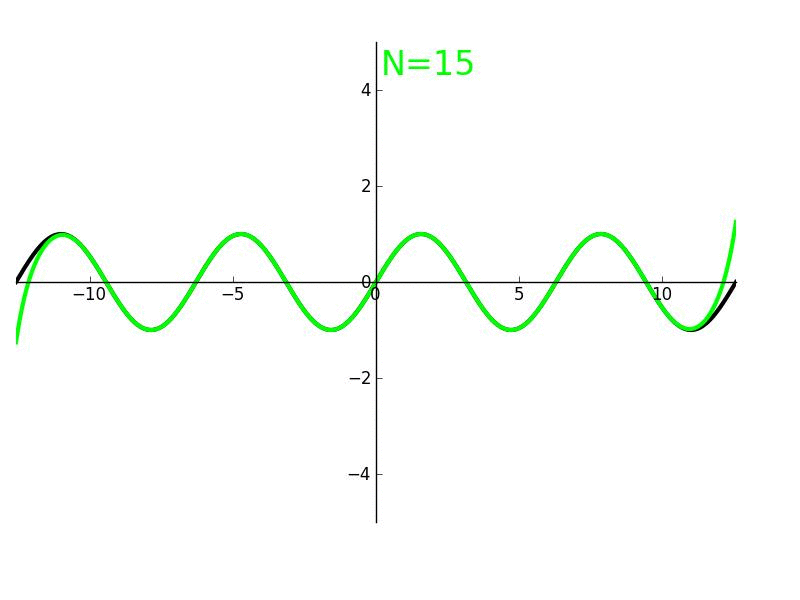
Her ikisi de genellikle bir nokta etrafındaki bir fonksiyonun n’inci derece türevleriyle eşleşecek şekilde formüle edilmiş bir toplamı tanımlamak için kullanılır. Taylor serisi, bu toplamın sonsuz olduğunu belirtirken, Taylor teoremi (polinom), herhangi bir n pozitif tamsayı değerini alabilir.
Bir Taylor polinomunun sınırlı sayıda terimi varken, bir Taylor serisinde sonsuz sayıda terim vardır. Taylor polinomları, Taylors serisinin kısmi toplamlarıdır. Örneğin, ex için x = 0 ile ilgili Taylor serisi → 1 + x + x2/2! + x3/3! + x4/4! + …. dır.
Taylor polinomunun ex için x = 0 ile ilgili 3. derecesi → 1 + x + x2/2! + x3/3! dır.
Formulasyon
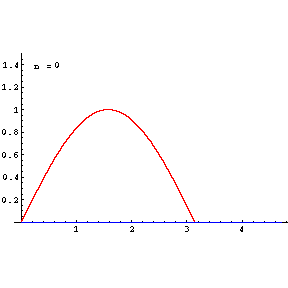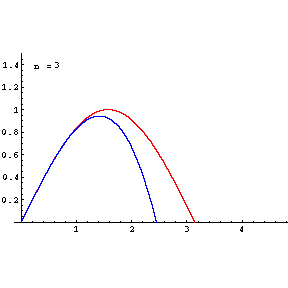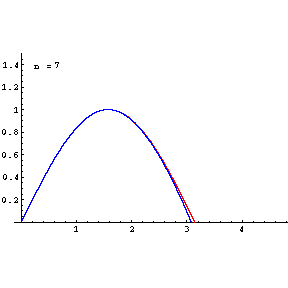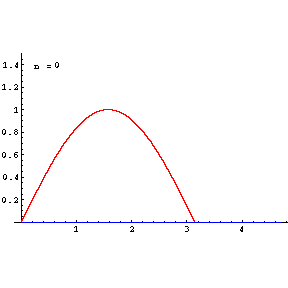
Taylor expansion’ın arkasındaki fikir her bir düzgün fonksiyonu sonsuz bir polinom terimlerinin toplamı olarak yeniden yazabileceğimizdir. F : R → R bir türevlenebilir fonksiyon ve a ∈ R olsun, o zaman a noktası etrafında f(x) fonksiyonunun bir Taylor serisi:
Taylor serisi (Power serisi olarak da bilinir), burada n! n’nin faktöriyelini belirtir, şu şekilde yazılabilir;
Özellikle türevlerin → a = 0 olduğu nokta sıfır ise, bu genişleme Taylor serisinin bu özel durumuna 18. yüzyıldan itibaren Colin Maclaurin tarafından yaygın kullanılan Maclaurin serisi olarak bilinir:
1/1-x için Maclaurin geometrik serisi, 1 + x + x2 + x3 + ⋯ dir, dolayısıyla a = 1’deki 1 / x için Taylor serisi → 1 − (x − 1) + (x − 1)2 − (x − 1)3 + ⋯. Maclaurin serisini entegre ederek, ln (1 – x) için Maclaurin serisini buluruz, burada ln doğal logaritmayı gösterir:
ln x için a = 1’deki karşılık gelen Taylor serisi:
ve daha genel olarak, sıfır olmayan rastgele bir a noktasında ln x için karşılık gelen Taylor serisi:
Üstel fonksiyon için Maclaurin serisi → ex = 1 + x + x2/2! + x3/3! + x4/4! + x5/5! + …
Örnek Olarak
e2 = 2.71828… × 2.71828… = 7.389056…
Sonsuz serinin daha fazla terimini deneyelim:
| Terms | Result | |
|---|---|---|
| 1+2 | 3 | |
| 1+2+22/2! | 5 | |
| 1+2+22/2!+23/3! | 6.3333… | |
| 1+2+22/2!+23/3!+24/4! | 7 | |
| 1+2+22/2!+23/3!+24/4!+25/5! | 7.2666… | |
| 1+2+22/2!+23/3!+24/4!+25/5!+26/6! | 7.3555… | |
| 1+2+22/2!+23/3!+24/4!+25/5!+26/6!+27/7! | 7.3809… | |
| 1+2+22/2!+23/3!+24/4!+25/5!+26/6!+27/7!+28/8! | 7.3873… |
Taylor serisi x’teki fonksiyona yakınsar ise, Taylor polinomunun daha yüksek derecesi x’teki fonksiyona daha iyi yaklaşım verir.
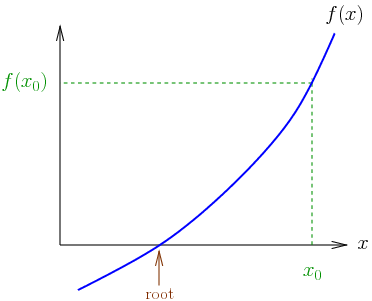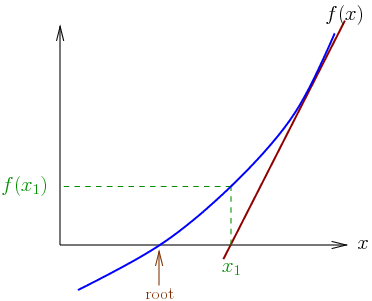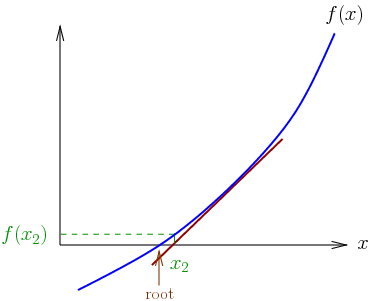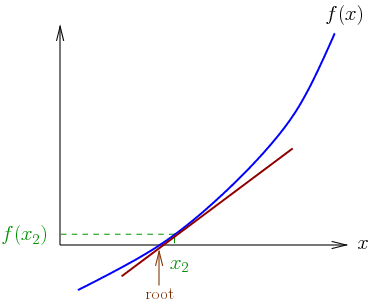
Newton’s Metodu ve Kök Bulma
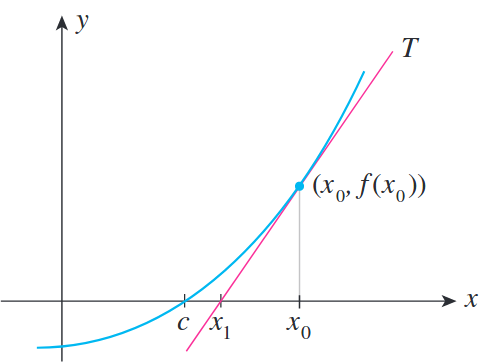
- Newton yöntemi denklemlere çözümleri yaklaştırmak (kök bulmak) için yinelemeli bir yöntemdir. Eğer f pozitif tanımlı ikinci dereceden bir fonksiyon ise, pratikte Newton yöntemi fonksiyonun minimumunu doğrudan bulabilir, fakat bu neredeyse hiç olmaz. Bunun yerine, Newton yöntemi f fonksiyonunun gerçekten ikinci dereceden olmadığı durumlarda uygulanabilir, fakat bölgesel olarak pozitif tanımlı ikinci dereceden olarak yaklaştırılabilir.
Daha fazla detay için Newton-Raphson Metodu
Özetlersek
Taylor Teorisi
Taylor teoremi, sing (x), log (x) vb. gibi sonsuz serilerin açılımı için kullanılır. Böylece bu fonksiyonların veya polinomların değerlerine yaklaşabiliriz.
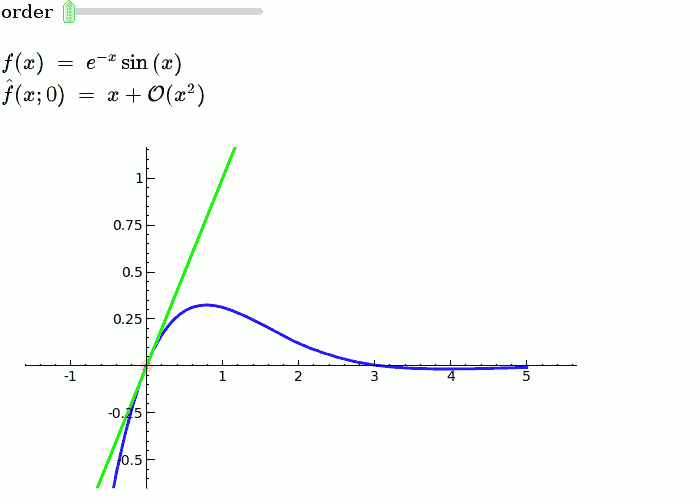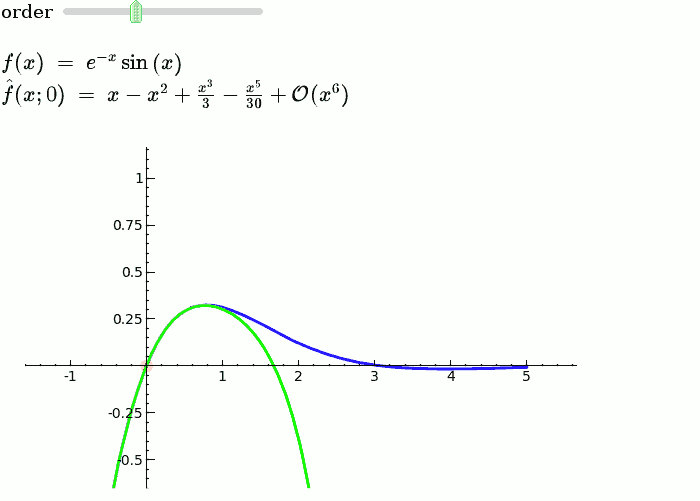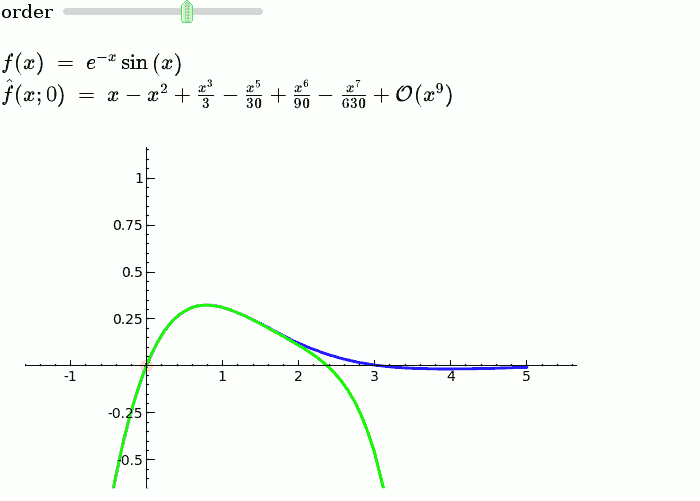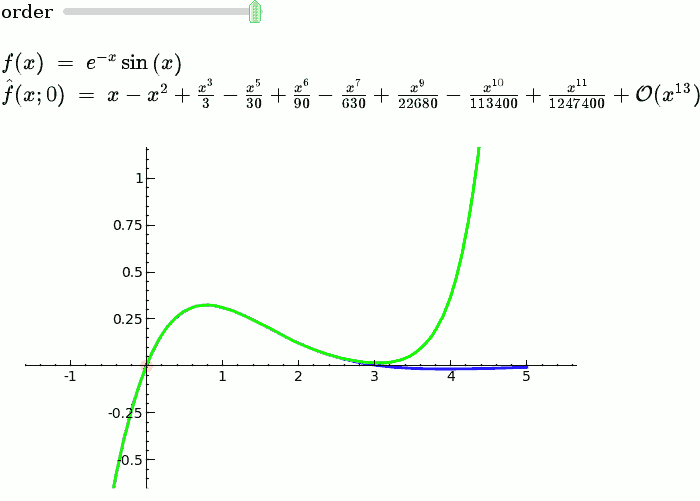
Yüksek matematikte, Taylor teoremi belirli bir nokta etrafında k-nth mertebeden bir Taylor polinomu ile k-kez türevlenebilir fonksiyonun bir yaklaşımını verir. Analitik fonksiyonlar için belirli bir noktadaki Taylor polinomları, bir noktada fonksiyonu tamamen belirleyen Taylor serisinin sonlu mertebeden kesilmeleridir. Farklı durumların birkaç versiyonu vardır ve bunlardan bazıları Taylor polinomu ile fonksiyonun yaklaşım hatası hakkında açık tahminler içerir.
Fonksiyonlar
1 – log(1+x)
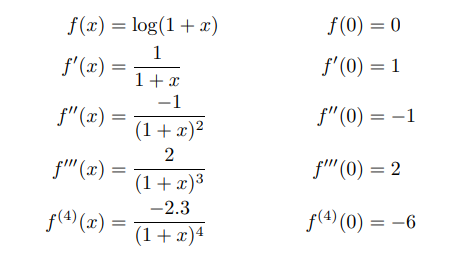
Serinin yakınsaması için bir formülasyon olarak → | x | <1;
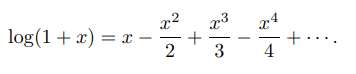
2 – ex

Fonksiyonda her k-zamanı için bir Taylor polinomu mevcut.
Serinin yakınsaması için bir formülasyon olarak → | x | <1:
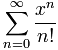
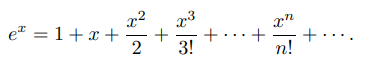
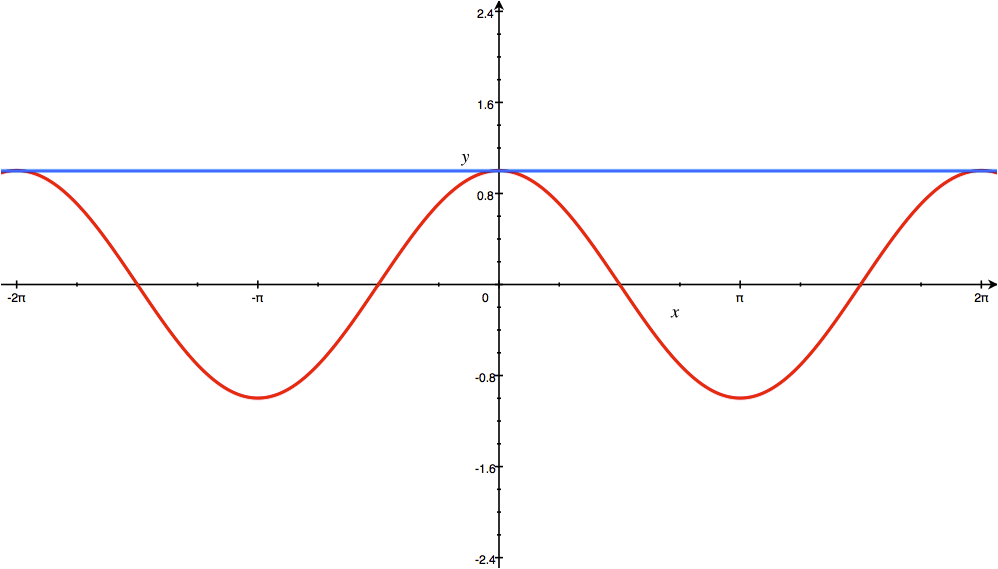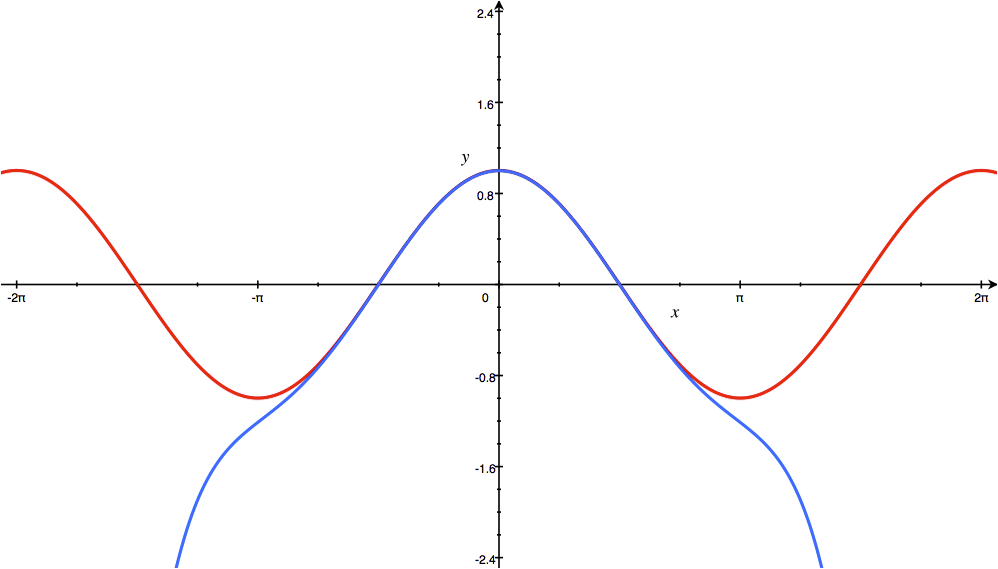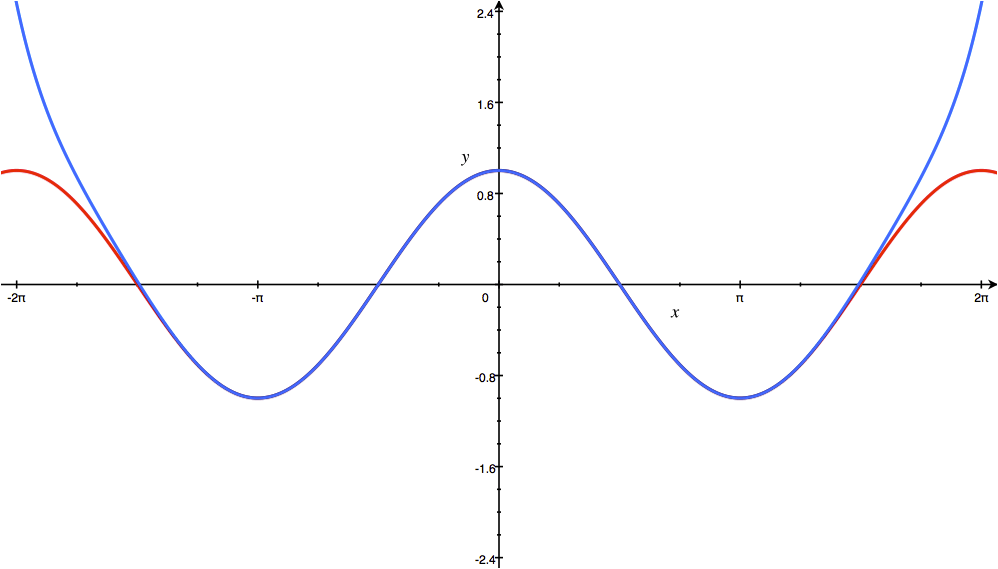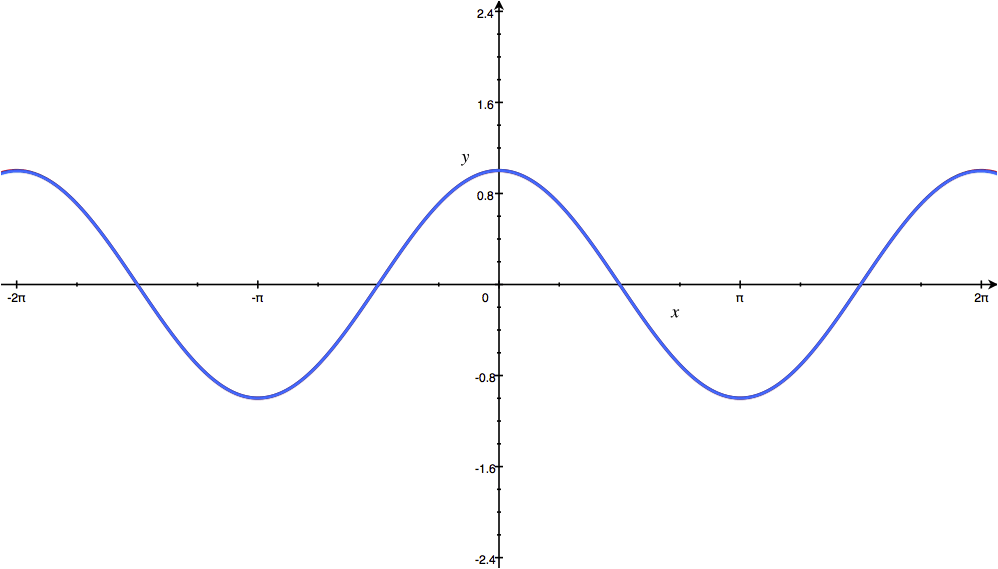
3 – cos x
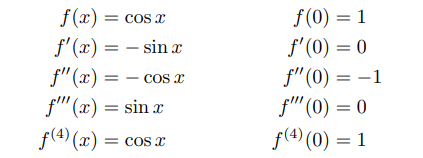
cos fonksiyonun türevi -sin ve sin fonksiyonunun türevi cos olarak hesaplarız.
cos(x) = cos(a) − [sin(a)/1!](x-a) − [cos(a)/2!](x-a)2 + [sin(a)/3!](x-a)3 + …
Eğer a = 0 ise, sonrasında cos(0) = 1 ve sin(0) = 0:
Serinin yakınsaması için bir formülasyon olarak → | x | <1:
![Taylor: Sigma n=0 to infinity of [ (-1)^n / (2n)! ] times x^(2n)](https://www.mathsisfun.com/algebra/images/taylor-cos-sigma.gif)
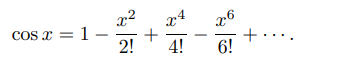
4 – sin x
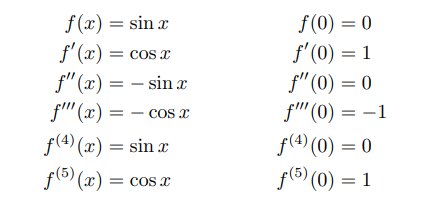
Serinin yakınsaması için bir formülasyon olarak → | x | <1:
![Taylor: Sigma n=0 to infinity of [ (-1)^n / (2n+1)! ] times x^(2n+1)](https://www.mathsisfun.com/algebra/images/taylor-sin-sigma.gif)
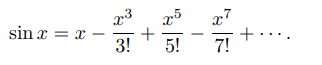
5 – 1/(1−x)
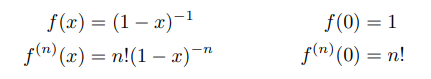
Serinin yakınsaması için bir formülasyon olarak → | x | <1:
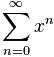
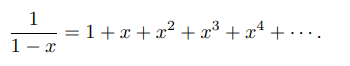
Kaynaklar:
le.ac.uk
brilliant.org
medium.com
feaforall.com
wikipedia.org
physicsforums.com
suzyahyah.github.io
visualizingmath.tumblr.com