Doğrusal (Linear) bir FEA çalışması, gerçek koşulları sadece bir dizi kısıtlayıcı koşul tanımlandığında simüle eder. Bunlar, tüm sapmaların çok küçük olduğunu ve yüklerin neden olduğu stress ve strain doğrusal ilişkilerinin (Hooke yasası) korunmasına izin verecek kadar küçük kalmasını içerir.
Doğrusal bir analiz, geometrinin kararsız bölgelerini tespit edemediği için hedefi kaçırabilir. Bu bölgelerde yük genliğindeki küçük bir değişiklik bile önemli ölçüde farklı deformasyonlara yol açabilir.
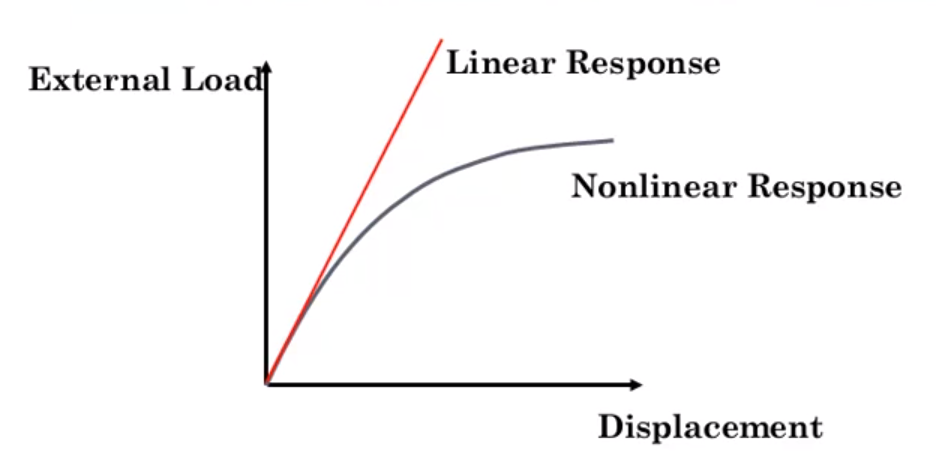
Lineer sonlu elemanlar yöntemi birçok şeyi basitleştirir. Örneğin, malzeme asla kopmayacak ve sonuç olarak modelde gerçekçi olmayan yüksek gerilimler meydana gelecektir. Ayrıca, doğrusal olmayan geometri dikkate alınmadığından başarısızlığı tahmin edemeyebilirsiniz.
FEA (Sonlu Elemanlar Analizi), FEM (Sonlu Elemanlar Yöntemi) adı verilen sayısal bir teknik kullanılarak herhangi bir gerçek fiziksel maddenin simülasyonudur.
Doğrusal Analiz Formülasyonu;
F = k • x
k = sertlik
x = yer değiştirme/sapma
F = kuvvet
Doğrusal analizde sertliğin sabit bir matrisi/katsayısı vardır. Dolayısıyla kuvvet ve yer değiştirme birbiriyle doğru orantılıdır.
Doğrusal Olmayan (Nonlinear) Analiz
Doğrusal olmayan etkiler, geometrik, malzeme ve temastan kaynaklanır. Bu etkiler, yük uygulaması sırasında sabit olmayan bir sertlik matrisine yol açar. Bu sertlik matrisi, sabit kaldığı doğrusal analizden farklıdır.
Doğrusal Olmayan Analiz Formülasyonu;
F = k • x → F = (k0 + k1• x + k2 • x2 +…) • x
k = sertlik
x = yer değiştirme/sapma
F = kuvvet
Doğrusal olmayan analizde, sertlik matrisi/katsayısı her iterasyon bazında güncellenir.
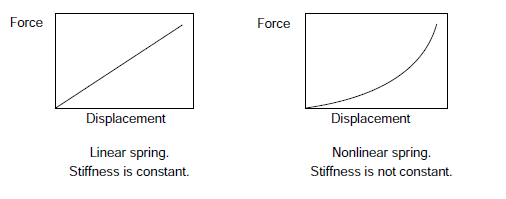
Geometrinin durumuna göre değişen ve malzemenin özelliklerine bağlı olan sertlik değeri, ilk sertlik matrisi analiz sırasından itibaren sürekli güncellenmeden kullanılamaz.
Problemlerin sayısal çözümleri doğrusal olmama (nonlinearities) içerir.
Doğrusal Olmayan Durum Türleri
3 farklı doğrusal olmama durumu vardır.
- Geometrinin Doğrusal Olmaması (Geometric Nonlinerity)
- Malzemenin Doğrusal Olmaması (Material Nonlinerity)
- Kontağın Doğrusal Olmaması (Contact Nonlinerity)
Geometrinin Doğrusal Olmaması
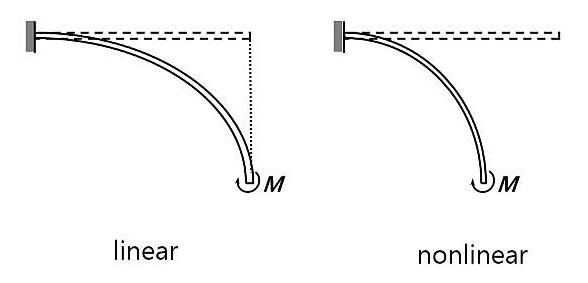
Geometrik doğrusal olmamada, yapı deforme olduğunda geometride meydana gelen değişiklikler, yapıcı ve denge denklemlerinin formüle edilmesi dikkate alınır. Metal şekillendirme, tıbbi cihaz ve benzeri analizler gibi birçok ileri mühendislik uygulaması geometrik doğrusal olmama durmununa dayanarak, büyük deformasyon analizilerinin kullanılmasını gerektirir.
Çoğu zaman geometrik olarak doğrusal olmayan problemler büyük yer değiştirme etkileri ile ilişkilidir. Geometrik doğrusal olmama durumu küçük yer değiştirmeler de içerebilir.
Küçük yer değiştirme/deformasyon (Small deformation): Son derece küçük ve ihmal edilebilir. 1 metre uzunluğundaki çubuğun 1 mm uzaması.
Büyük yer değiştirme/deformasyon (Finite/large deformation): Küçük ve ihmal edilebilir olmayan. 1 metre uzunluğundaki çubuğun 10 mm uzaması.
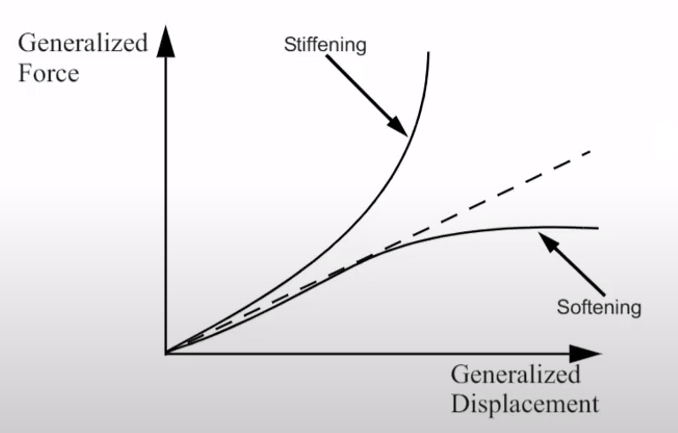
Eğer bir yapıdaki malzeme, değişen sertlik gibi yeterince büyük deformasyon yaşarsa, bu olay geometrik doğrusal olmama olarak adlandırılır. Bu durum yapının sertleştirilmiş veya yumuşatılmış bir şekilde tepki vermesine neden olur.
Malzemenin Doğrusal Olmaması
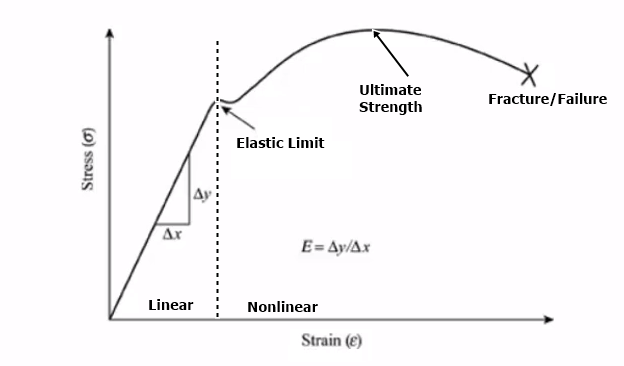
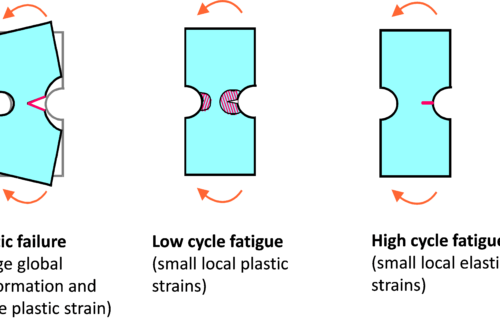
Malzemenin doğrusalsızlığı, anlık deformasyon, sıcaklık, basınç vb. gibi değerler ile malzemenin doğrusal olmayan davranışlarını içerir. Bazı doğrusal olmayan malzeme modelleri büyük gerinim, gerilme-gerinim ilişkisi, elastoplastisite, plastiklik, sünme ve aşırı esnekliktir.
Kontağın Doğrusal Olmaması
Kontak, bir tür “durum değiştirme” dir. Gövdeler birbirleriyle temas ettiğinde veya teması bıraktığı anda sertlikte ani bir değişiklik meydana gelebilir. Analiz sırasındaki bu hareket, analizdeki bileşenler arasındaki temasın değişen doğasının bir sonucudur.
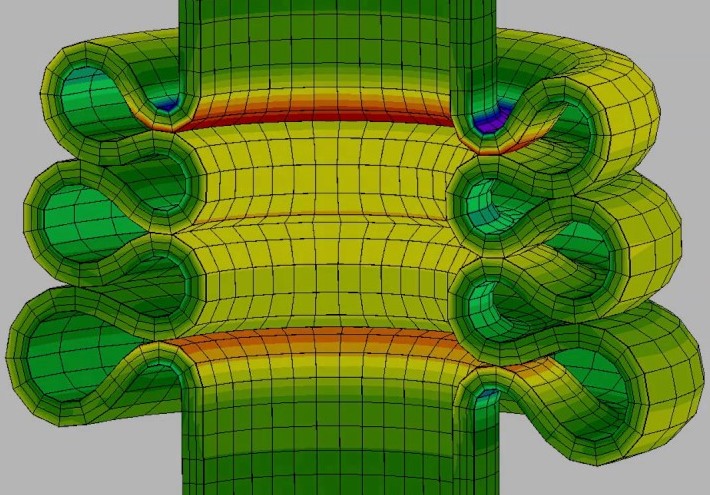
Doğrusal olmayan temasta üç ana alan dikkate alınır; “Kontak Uygulamaları”, “Kontak Kinematiği” ve “Kontak Algoritmaları”.
Modelde kinematik kısıtlamalar ayarlanmışsa, bir sistemdeki kısıtlama doğrusal olmama durumu oluşabilir. Modelin kinematik serbestlik derecesi kısıtlanabilir.
Kaynaklar:
researchgate.net
homes.civil.aau.dk Magazines