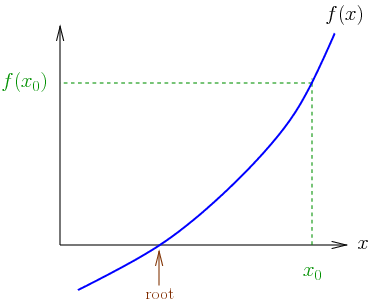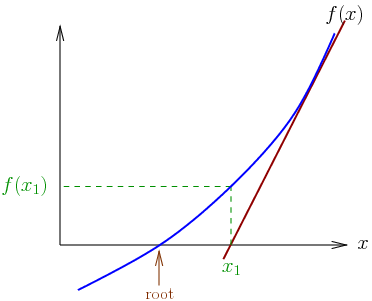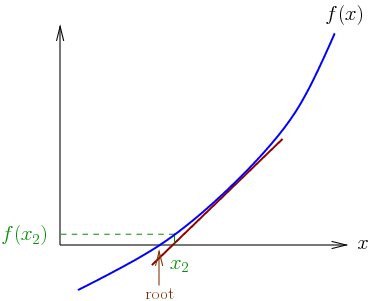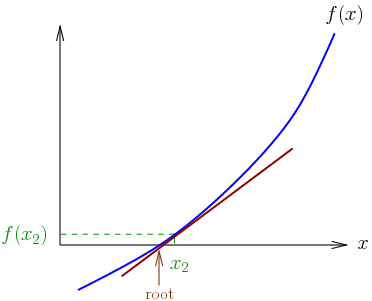
In numerical analysis, the Newton–Raphson method (also known as Newton’s method), named after Isaac Newton and Joseph Raphson, is a method for finding successively and quickly better approximations for the roots of real-valued functions. The Newton-Raphson method is a powerful technique for solving equations numerically. It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it. The idea starts with an initial guess which is reasonably close to the true root, then to approximate the function by its tangent line, and to compute the x-intercept of this tangent line by elementary algebra. This x-intercept will typically be a better approximation to…