The Taylor expansion is one of the most useful ideas in mathematics. Most functions and polynomials are generally smooth to solve. Polynomials are easier to work than almost any other sort of function, and polynomials are largely able to approximate to functions. The Taylor formula gives us an equation for the polynomial expansion for nearly every smooth function of f.
Taylor Series
In mathematics, the Taylor series of a function is an infinite sum of terms that are expressed in terms of the function’s derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor’s series are named after Brook Taylor who introduced them in 1715.
Taylor’s Theorem
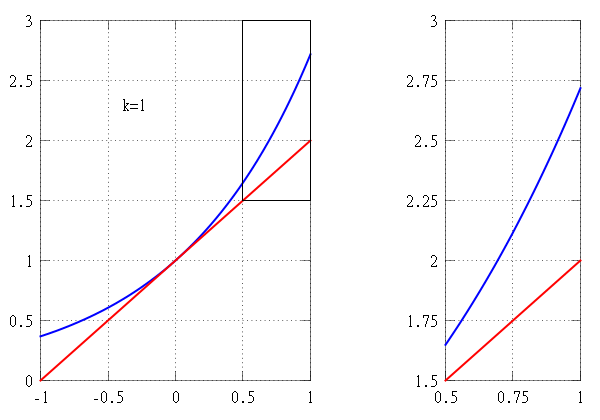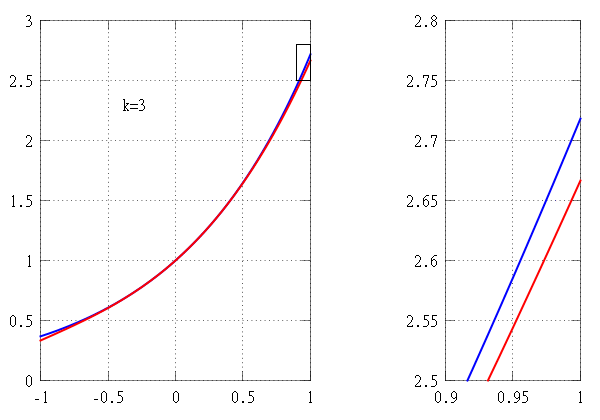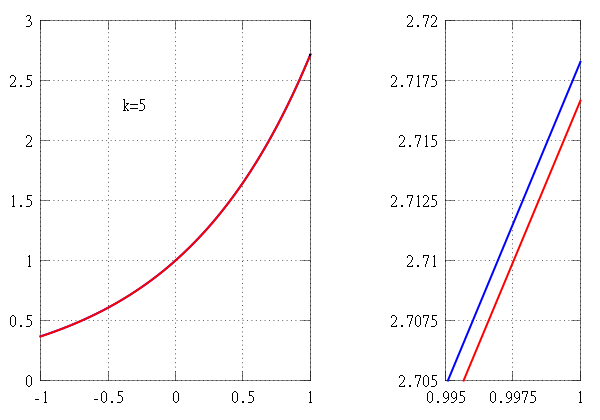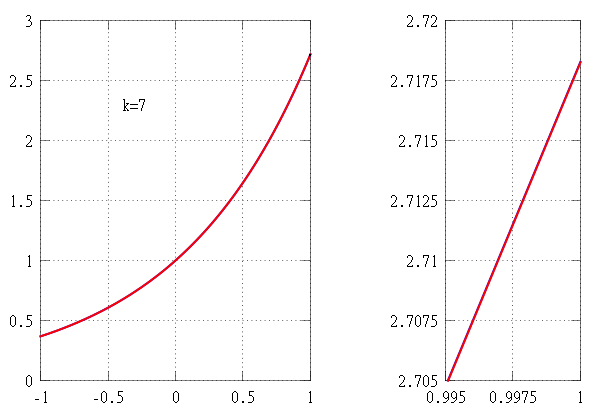
In calculus, Taylor’s theorem gives an approximation of a k-times differentiable function around a given point by a polynomial of degree k, called the kth order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order k of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor’s theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.
Taylor’s theorem gives simple arithmetic formulas to accurately compute values of many transcendental functions such as the exponential function and trigonometric functions. It is the starting point of the study of analytic functions as well as in numerical analysis and mathematical physics.
The partial sum formed by the first n + 1 terms of a Taylor series is a polynomial of degree n that is called the nth Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as n increases.
Taylor Series vs Taylor Theorem
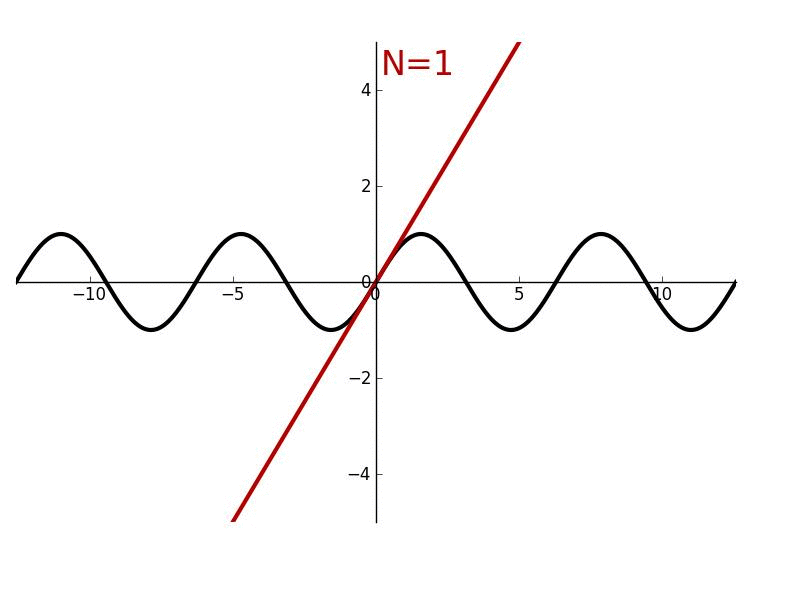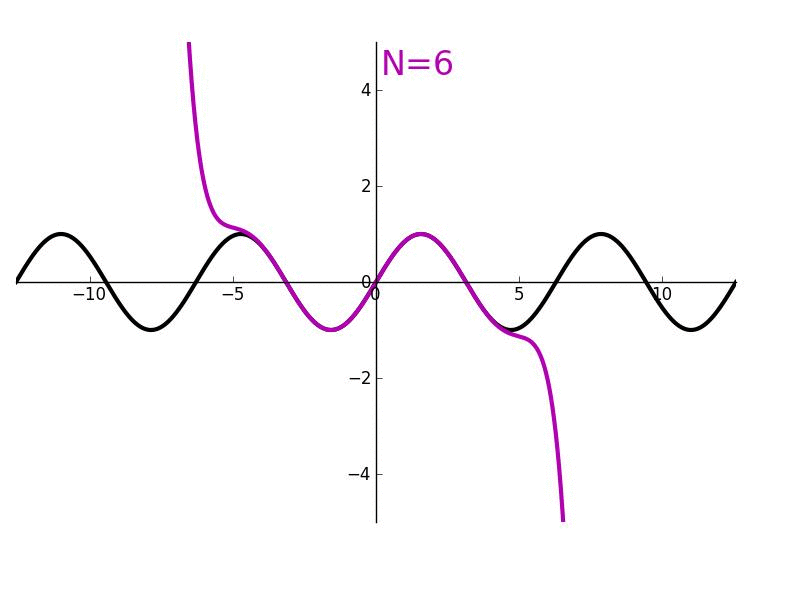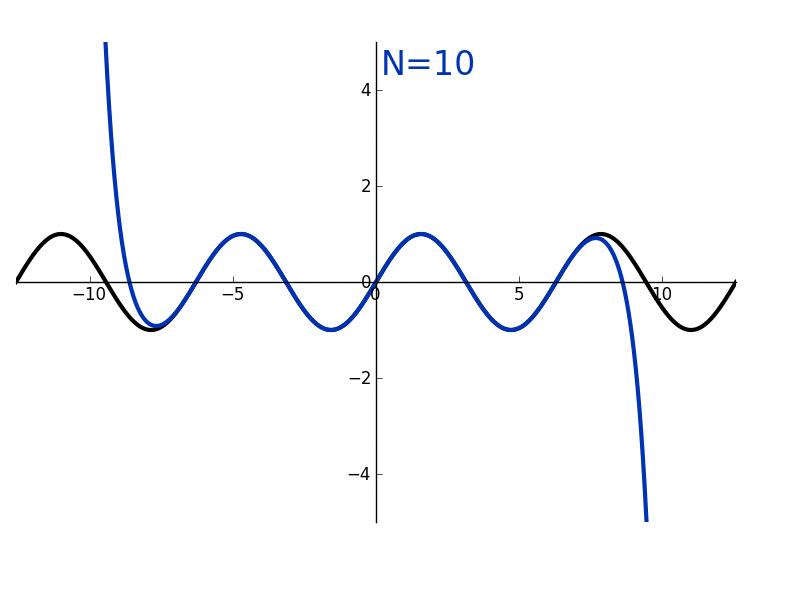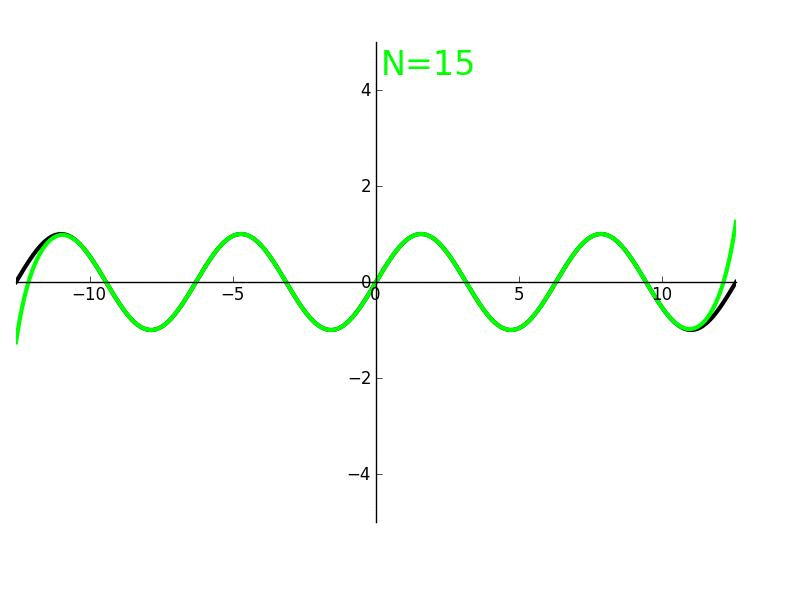
Both are commonly used to describe a sum to n formulated to match up to the nth order derivatives of a function around a point. Taylor series implies that this sum is infinite, while Taylor theorem (polynomial) can take any positive integer value of n.
A Taylor polynomial has a finite number of terms, whereas a Taylor series has infinitely many terms. The Taylor polynomials are the partial sums of the Taylors series. For instance, the Taylor series of ex about x = 0 is → 1 + x + x2/2! + x3/3! + x4/4! + ….
The 3th degree for Taylor polynomial of ex about x = 0 is → 1 + x + x2/2! + x3/3!
Formulation
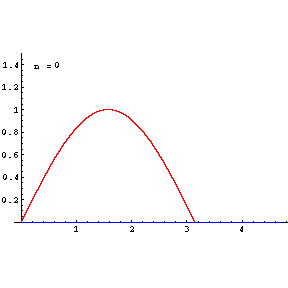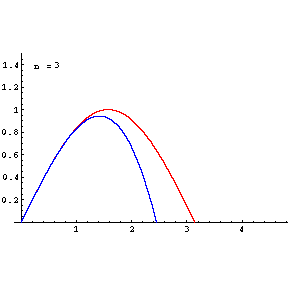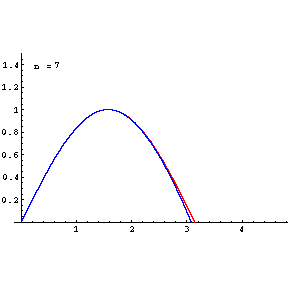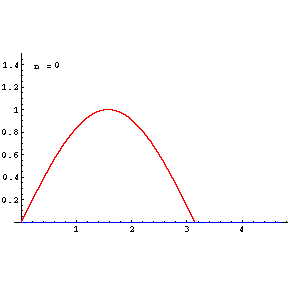
The idea behind the Taylor expansion is that we can rewrite every smooth function as an infinite sum of polynomial terms. Let f : R → R is a differentiable function and a ∈ R, then a Taylor series of the function f(x) around the point a is:
The Taylor series (also known as Power series), where n! denotes the factorial of n, can be written as;
In particular, if zero is the point, where the derivatives → a = 0, then the expansion is known as the Maclaurin series after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century, and thus is given by:
The Maclaurin series for 1 / 1 – x is the geometric series of 1 + x + x2 + x3 + ⋯ , so the Taylor series for 1 / x at a = 1 is → 1 − (x − 1) + (x − 1)2 − (x − 1)3 + ⋯ . By integrating the Maclaurin series, we find the Maclaurin series for ln(1 − x), where ln denotes the natural logarithm:
The corresponding Taylor series for ln x at a = 1 is:
and more generally, the corresponding Taylor series for ln x at an arbitrary nonzero point a is:
The Maclaurin series for the exponential function → ex = 1 + x + x2/2! + x3/3! + x4/4! + x5/5! + …
Exemplary
e2 = 2.71828… × 2.71828… = 7.389056…
let’s try more terms of infinite series:
| Terms | Result | |
|---|---|---|
| 1+2 | 3 | |
| 1+2+22/2! | 5 | |
| 1+2+22/2!+23/3! | 6.3333… | |
| 1+2+22/2!+23/3!+24/4! | 7 | |
| 1+2+22/2!+23/3!+24/4!+25/5! | 7.2666… | |
| 1+2+22/2!+23/3!+24/4!+25/5!+26/6! | 7.3555… | |
| 1+2+22/2!+23/3!+24/4!+25/5!+26/6!+27/7! | 7.3809… | |
| 1+2+22/2!+23/3!+24/4!+25/5!+26/6!+27/7!+28/8! | 7.3873… |
The higher degree of the Taylor polynomial gives better approximation to the function at x, if the Taylor series converges to the function at x.
Newton’s Method and Root Finding
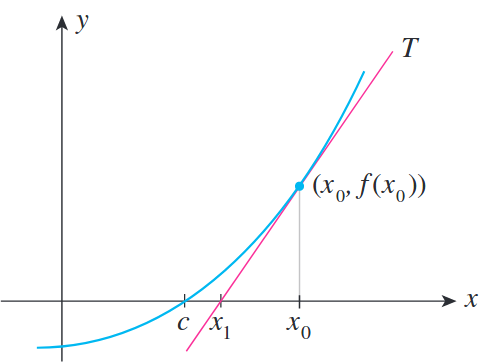
- Newton’s method is an iterative method for approximating solutions (finding roots) to equations. If f is a positive definite quadratic function, Newton’s method can find the minimum of the function directly in practice, this almost never happens. Instead, Newton’s method can be applied when the function f is not truly quadratic but, it can be locally approximated as a positive definite quadratic.
For more detail about The Newton-Raphson Method
In Conclusion
Taylor’s Theorem
Taylor’s theorem is used for the expansion of the infinite series such as sing(x), log(x) etc. So that we can approximate the values of these functions or polynomials.
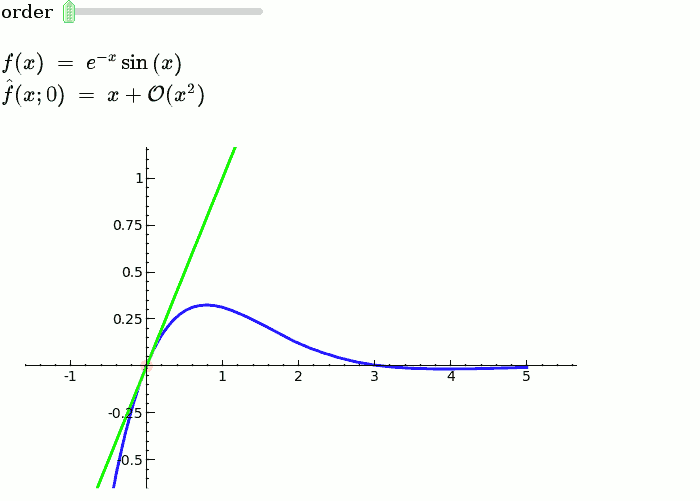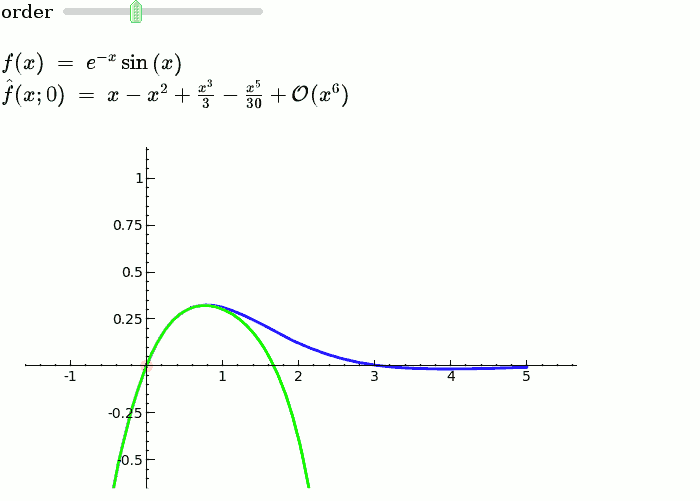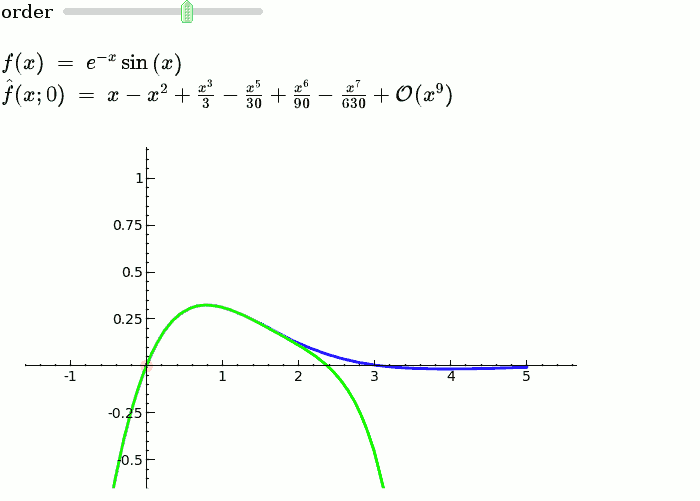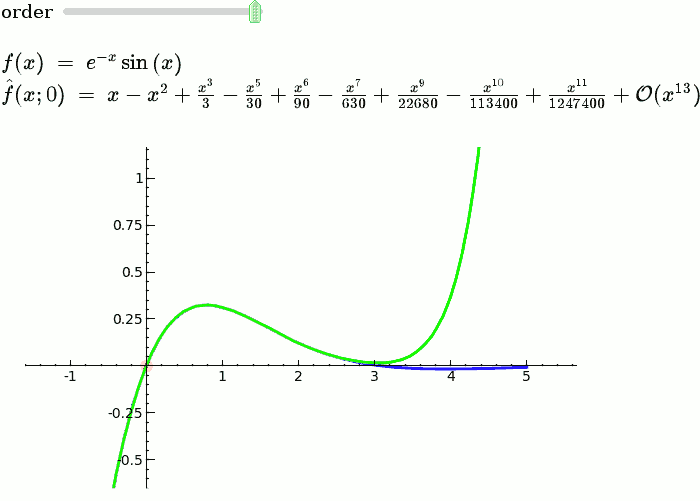
In higher mathematics, Taylor’s theorem gives an approximation of k-times differentiable function around a given point by a with k-nth order Taylor polynomial. For analytic functions, the Taylor polynomials at a given point are finite order truncations of its Taylor series, which completely determines the function in some point. There are several versions of different situations, and some of them contain explicit estimates on the approximation error of the function by its Taylor polynomial.
Functions
1 – log(1+x)
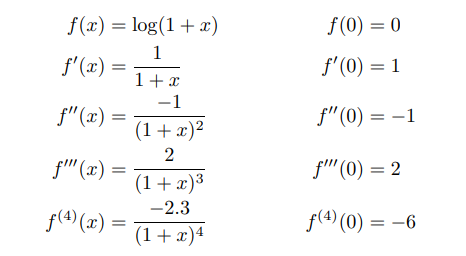
as a formulation for the convergence of the series → |x| < 1;
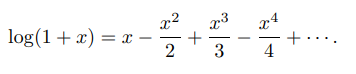
2 – ex

For each k-time we have a Taylor polynomial for the function.
as a formulation → |x| < 1;
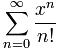
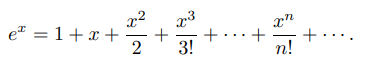
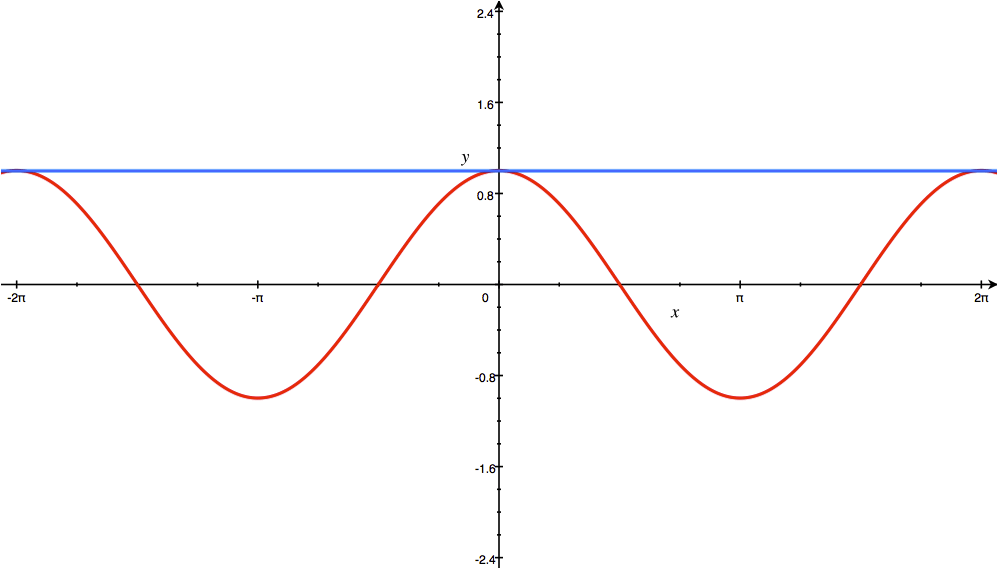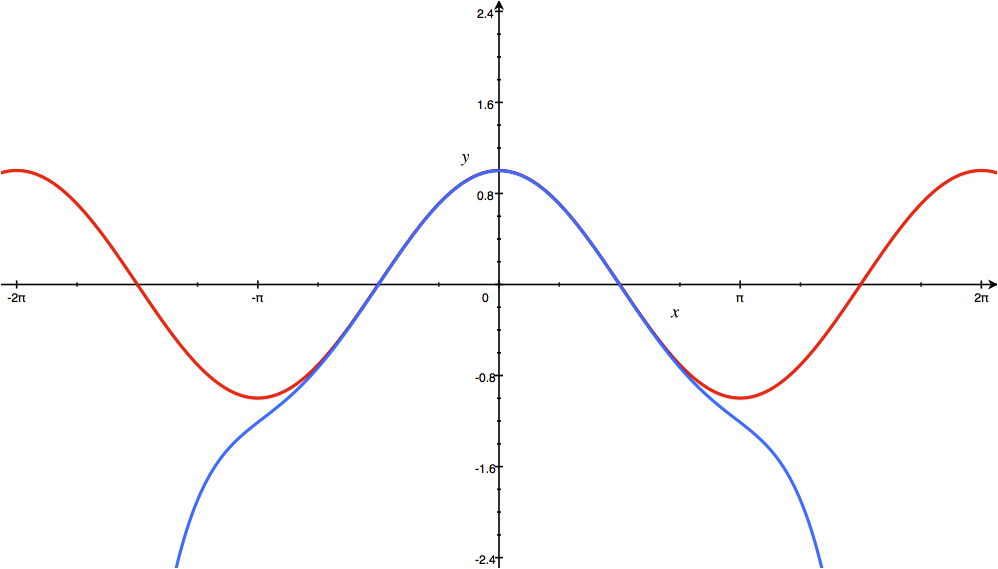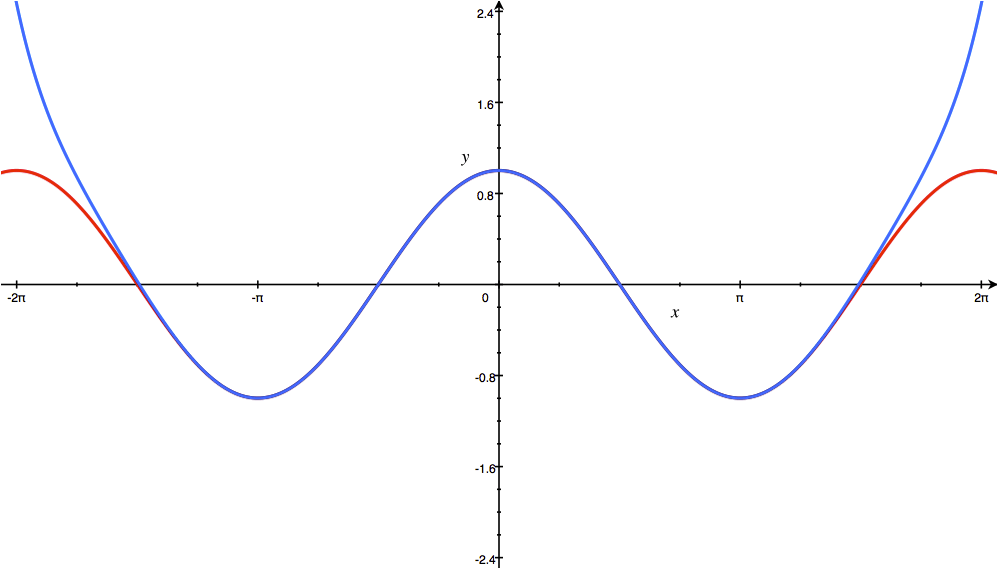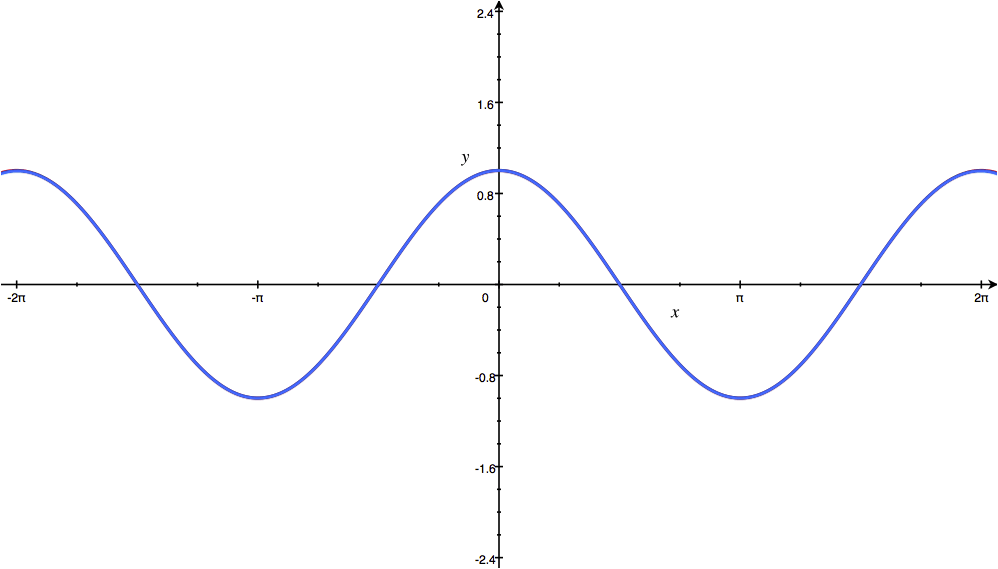
3 – cos x
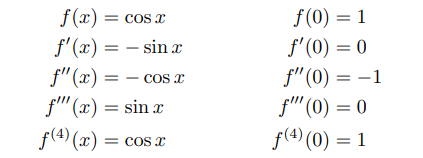
The derivative of cos is −sin, and the derivative of sin is cos;
cos(x) = cos(a) − [sin(a)/1!](x-a) − [cos(a)/2!](x-a)2 + [sin(a)/3!](x-a)3 + …
If a = 0, then cos(0) = 1 and sin(0) = 0:
as a formulation → |x| < 1;
![Taylor: Sigma n=0 to infinity of [ (-1)^n / (2n)! ] times x^(2n)](https://www.mathsisfun.com/algebra/images/taylor-cos-sigma.gif)
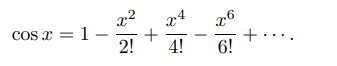
4 – sin x
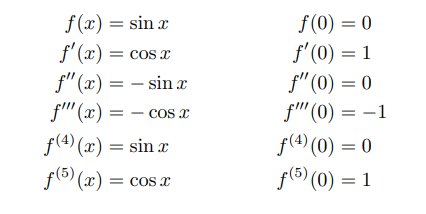
as a formulation → |x| < 1;
![Taylor: Sigma n=0 to infinity of [ (-1)^n / (2n+1)! ] times x^(2n+1)](https://www.mathsisfun.com/algebra/images/taylor-sin-sigma.gif)
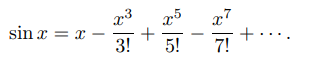
5 – 1/(1−x)
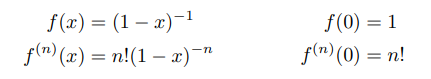
as a formulation → |x| < 1;
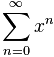
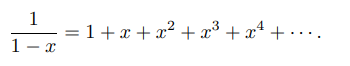
Sources:
le.ac.uk
brilliant.org
medium.com
feaforall.com
wikipedia.org
physicsforums.com
suzyahyah.github.io
visualizingmath.tumblr.com