In numerical analysis, the Newton–Raphson method (also known as Newton’s method), named after Isaac Newton and Joseph Raphson, is a method for finding successively and quickly better approximations for the roots of real-valued functions.
The Newton-Raphson method is a powerful technique for solving equations numerically. It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it.
The idea starts with an initial guess which is reasonably close to the true root, then to approximate the function by its tangent line, and to compute the x-intercept of this tangent line by elementary algebra. This x-intercept will typically be a better approximation to the original function’s root than the first guess, and the method can be iterated.

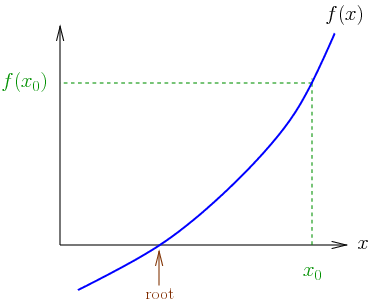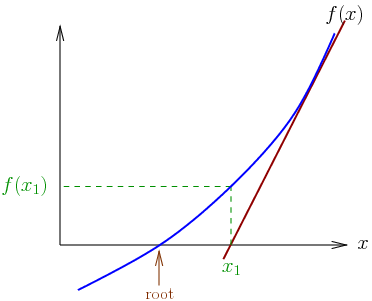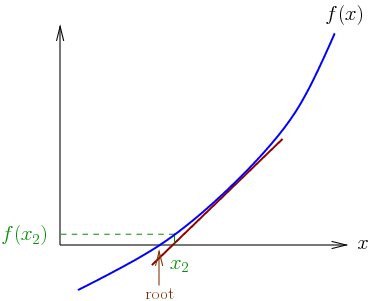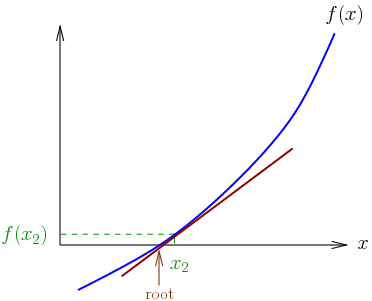
The method starts with a function f defined over the real numbers x, the function’s derivative f ′, and an initial guess x0 for a root of the function f. If the function satisfies sufficient assumptions, and the initial guess is close, then a better approximation x1 is;
There is a better approximation of the root than x0. Geometrically, (x1, 0) is the intersection of the x-axis and the tangent of the graph of f at (x0, f(x0)). The improved guess is the unique root of the linear approximation at the initial point. The process is repeated as the process is repeated as , until a sufficiently accurate value is reached.
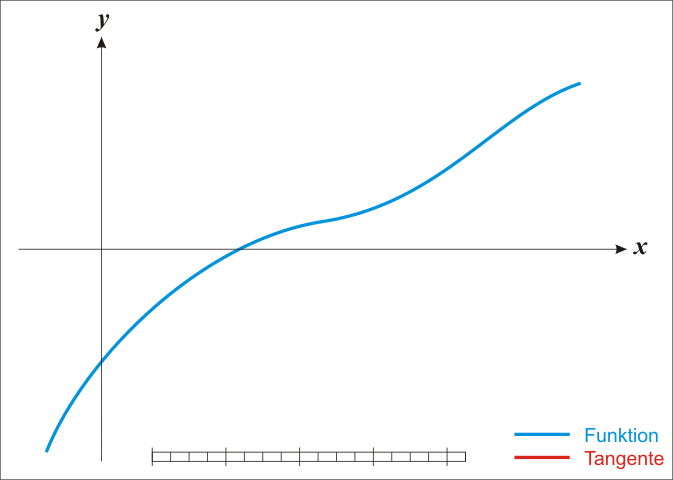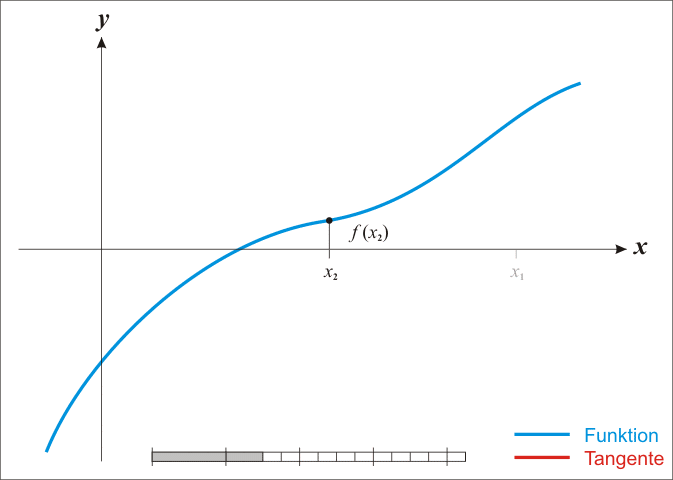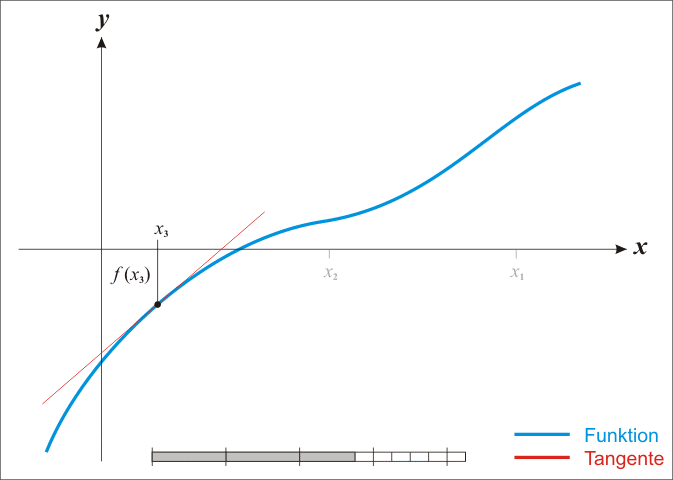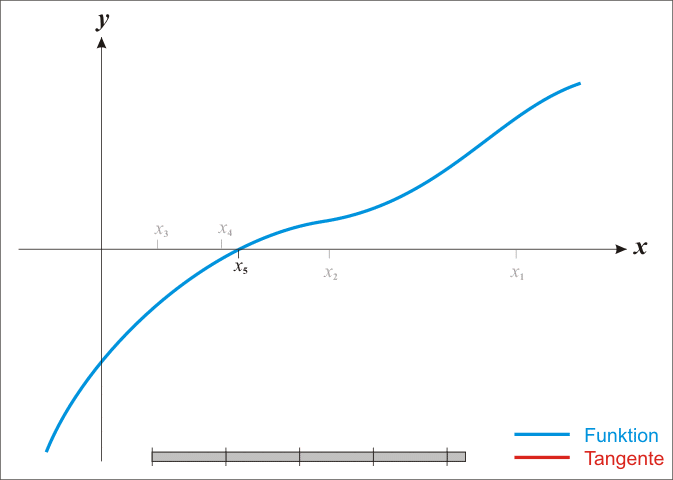
The idea of the method follows that one of the approach starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line, and one computes the x-intercept of this tangent line. The method can also be extended to complex functions and to systems of equations.
In general, the convergence is quadratic; as the method converges on the root, the difference between the root and the approximation is squared at each step.
Also, there are some difficulties with the method; if the assumptions made in the proof of quadratic convergence of Newton’s method are not met, slow convergence for roots of multiplicity.
The Base of Formulation
The Newton-Raphson method is a root-finding algorithm that uses the first few terms of the Taylor series of a function. To solve the equation f(x) = 0, first Taylor expansion of the function f (x) is considered,
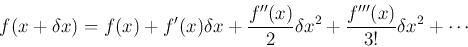
If f(x) is linear, only the first two terms, the constant and linear terms are non-zero,
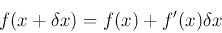
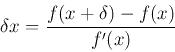
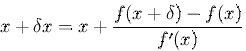
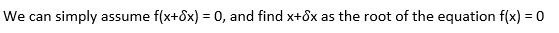
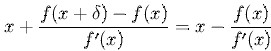
If f(x) is nonlinear, Xn+1 is an improved approximation of the root based on the previous approximation Xn, the the root will be approached by this iteration,
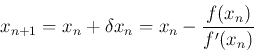
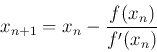
Exemplary
Let’s solve (2x^3)-2x-1 = 0. In this case f(x) = (2x^3)-2x-1, so f′(x) = (6x^2)-2.
So the formula becomes,
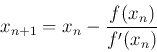
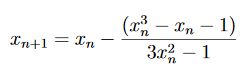
Need to decide on an appropriate initial guess x0 for this problem. f(1) = −1<0 and f(2) = 11>0. Therefore, a root of f(x)=0 must exist between 1 and 2. Let us take x0 =1 as our initial guess. Then
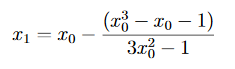
and with x0 = 1 we get x1 = 1.25.
Now
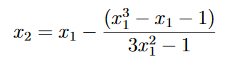
and with x1 = 1.25 we get x2 = 1.1949. For the next stage,
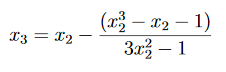
x3=1.1915. Carrying on, we find that x4=1.191487884, x5=1.191487883, etc.
We can stop when the digits stop changing to the required degree of accuracy. We conclude that the root is 1.191487883.
In Conclusion
- A nonlinear structure can be analysed using an iterative series of linear approximations with corrections.
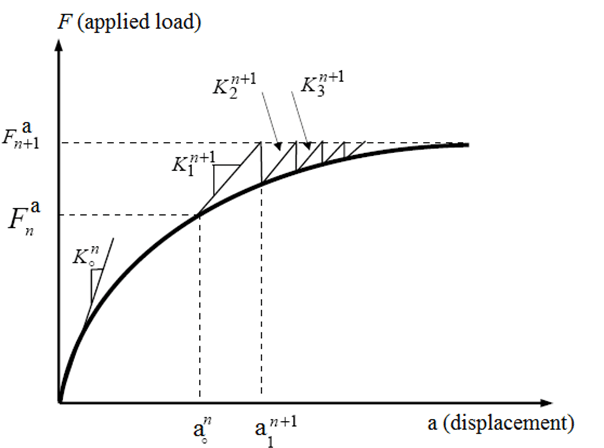
- Some FEA softwares use an iterative process called the Newton-Raphson Method. Each iteration is known as an equilibrium iteration.
- In nonlinear analysis, relationship between load and displacement cannot be determined with a single solution based on initial stiffness.
- If residual forces are within an acceptable tolerance, the solution is converged.
- If residual forces are not within an acceptable tolerance, the solution is not converged, so a new target stiffness matrix is assembled and the process is repeated.
Equilibrium iteration:
In nonlinear solution, equilibrium iterations are corrective solutions needed for convergence using the Newton-Raphson Method.
Halley’s method will be mentioned detailedly on some other articles.
Sources:
wikipedia.org
sciencedirect.com
personal.maths.surrey.ac.uk