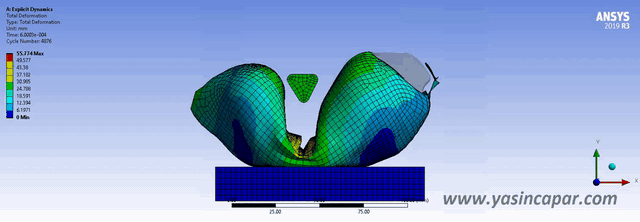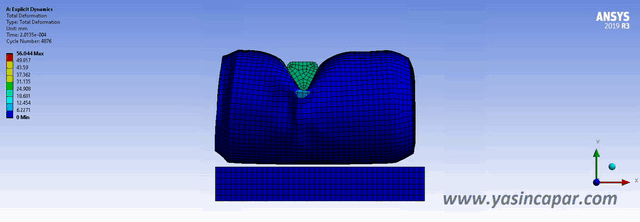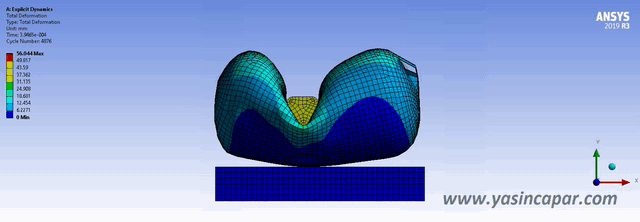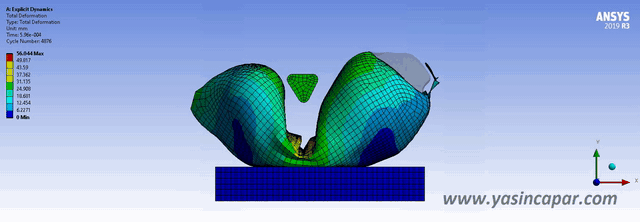
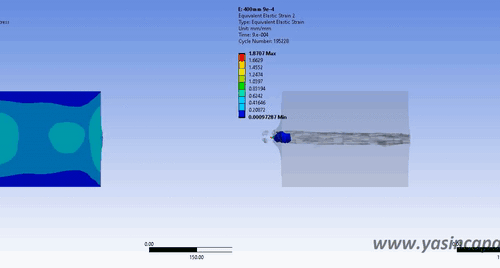
Explicit and implicit methods are used in numerical analysis for obtaining numerical approximations to solve solutions of time-dependent ordinary and partial differential equations which require computer simulations of physical processes. Explicit methods calculate the state of a system at a later time from the state of the system at the current time, while implicit methods find a solution by solving an equation involving both the current state of the system and the later one. For all nonlinear and dynamic analyses, incremental loads are needed. Commonly, ‘implicit’ and ‘explicit’ methods are used to solve these problems. In static analysis, there is no effect of mass (inertia) or damping. In dynamic analysis,…