Implicit vs Explicit Approach in FEM

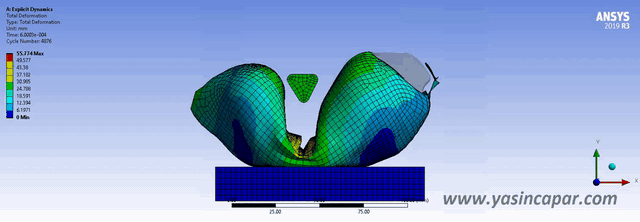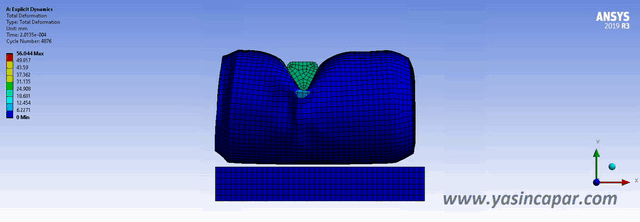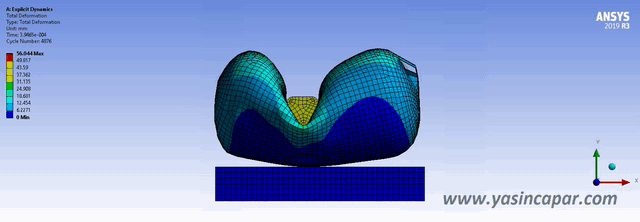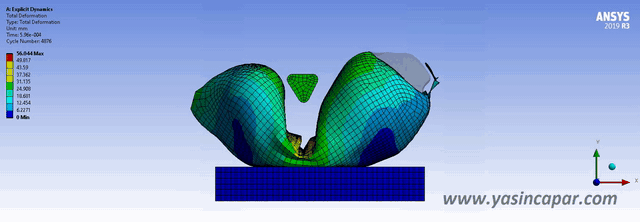
Explicit and implicit methods are used in numerical analysis for obtaining numerical approximations to solve solutions of time-dependent ordinary and partial differential equations which require computer simulations of physical processes.

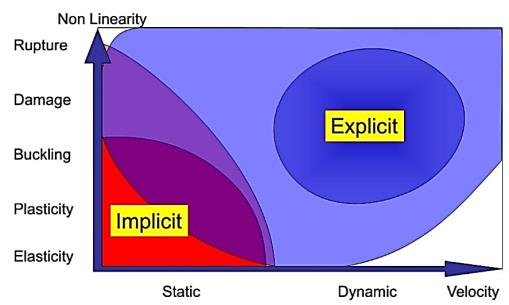
Explicit methods calculate the state of a system at a later time from the state of the system at the current time, while implicit methods find a solution by solving an equation involving both the current state of the system and the later one.

For all nonlinear and dynamic analyses, incremental loads are needed. Commonly, ‘implicit’ and ‘explicit’ methods are used to solve these problems.

In static analysis, there is no effect of mass (inertia) or damping. In dynamic analysis, nodal forces associated with mass/inertia and damping are included. Dynamic analysis can be done via the explicit solver or the implicit solver.

In nonlinear implicit analysis, solution of each step requires iterations to establish equilibrium within a certain tolerance. In explicit analysis, no iteration is required as the nodal accelerations are solved directly.

Difference Between Implicit and Explicit?

Implicit and Explicit analysis dissociate in the approach to time incrementation. In Implicit analysis, each time increment has to converge, but users can set quite long time increments. Conversely, explicit analysis doesn’t have to converge each increment, but time increments must be super small for the accuracy of solution.

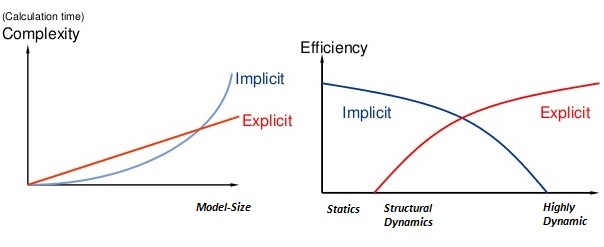
Implicit transient analysis has no time step limit. Implicit time steps are most often larger than explicit time steps.

Implicit and Explicit Problems

All of these problems are stated through mathematical partial differential equations. These matrix equations can be linear or nonlinear. In most structural problems, the nonlinear equations are considered in three categories:

• Material Nonlinearity:
• Geometric Nonlinearity:
• Boundary Nonlinearity:

For more detail: Nonlinearites

Formulations:

In linear problems, the partial differential equations reduce the matrix equation as:

[K]{x} = {f}

k = stiffness matrix
x = displacement/deflection
F = force

For non-linear static problems as:

[K(x)]{x} = {f} → [k₀ + k₁• x + k₂ • x² +…]{x} = {f}

For dynamic problems, the matrix equations become to:

[M]{x´´} + [C]{x´} + [K]{x} = {f}

x´ = velocity
x´´ = acceleration
C = damping matrix
M = mass matrix

When to use Implicit?

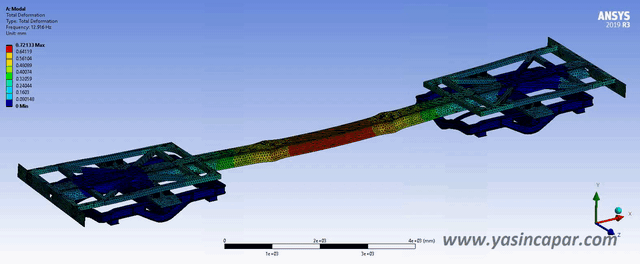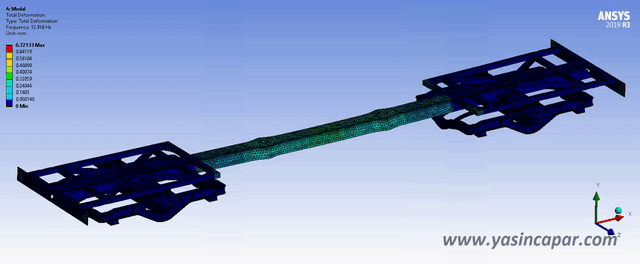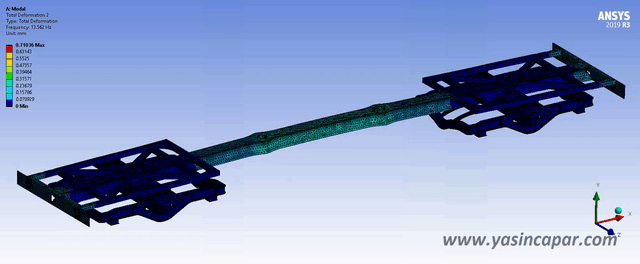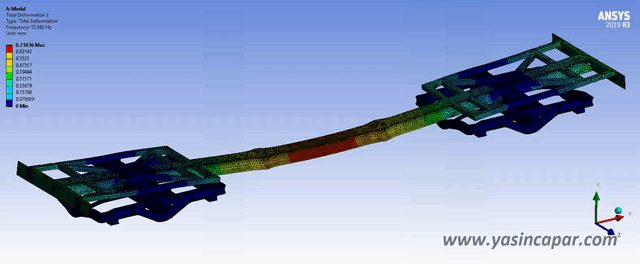
Implicit methods should be used when the boundary conditions affect the structure slowly, and the effects of strain rates are minimum. Once the increment of stress as a function of strain can be established, geometry can be analysed using implicit methods.

The global equilibrium in the model is established in each time increment. This means each increment has to converge.

After global equilibrium is converged, solver calculates all the local finite element variables (stresses, strain, etc.) for each increment.

• Pros: Since global equilibrium is verified at each time increments, those increments can be large.
• Cons: Each time, increments are computed slowly and needed to get to the global equilibrium.

When to use Explicit?

Explicit methods should be used when the strain rates is equal to 10^-3 per second or more. These events can be illustrated by some examples such as an automotive crash, ballistic explosion, drop and so on. In these cases, besides the variation of stress with strain, the rate of strain also needs to be considered.

There are no convergence criteria to check or iteration. The solver focus the calculation of local finite element variables.

Solver calculates all of the local finite element variables for given incrementation, and move to the next one.

• Pros: Each increment is calculated extremely fast.
• Cons: The time step has to be super small. Otherwise, it’s impossible to pursue this equilibrium.

Which is Better: Implicit or Explicit?

There is no easy answer to this question. Both of implicit and explicit solvers solve the same type of problems. Technically, both should produce the same outcome for all cases. We can analyse the same problem with both approaches. The vital difference between implicit and explicit is in the approach to time incrementation.

• The implicit analysis allows to be defined the time increment. Users can define how big the time increment should be. Iterations of this increment need to be completed for global equilibrium. Therefore, it requires some time to compute.
• Explicit time increments are calculated extremely fast.Simply because iteration for global equilibrium is not needed. Also, the time increment will not be able to adjusted by manually. Solver simply assumes an acceptable time increment and goes with it, which is super small.

In Conclusion

The implicit solver is really useful if conditions in your analysis happen relatively slow. Ideal analyses are generally longer than 1 second. The advantage is that the time increment can be set as big as users want.

1. Unknown x is found by inversion of stiffness matrix (K).
2. Newton-Raphson / Enforced equilibrium solutions.
3. Newton method is used.
4. More accurate
5. Extremely time-consuming for large models
6. Requires more computer storage
7. Strain rate is less than 10^-3 per second.
8. Good decision for structure dynamic types which load rates are slow;
   – Slowly applied displacements
   – Low frequency response
   – Vibration
   – Oscillation
   

The explicit solver is great for fast events (mostly less than 0.1 second) Explicit solver calculates how big the time increment should be and set the time increment. The speed of sound in material properties depends on density of material. This is called “mass scaling”. The time step in explicit depends on the mesh (element size and element quality), young modulus, and density.

1. Unknown x is found by inversion of mass matrix (M).
2. Direct solutions.
3. Central difference methods are used.
4. Less accurate
5. Computationally efficient for large models with short dynamic response time
6. Requires less computer storage.
7. Strain rate is equal or more than 10^-3 per second.
8. Good decision for structure dynamic types which are wave propagation;
   – Car crash
   – Blast effect
   – Drop
   – Metal stamping

Sources:
wikipedia.org
simscale.com
enterfea.com