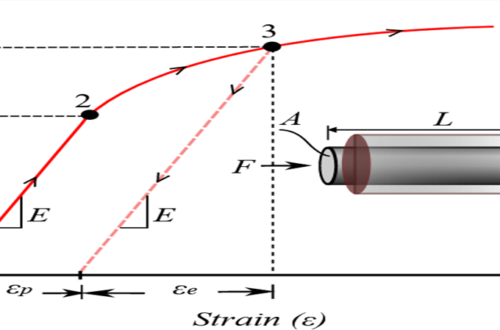
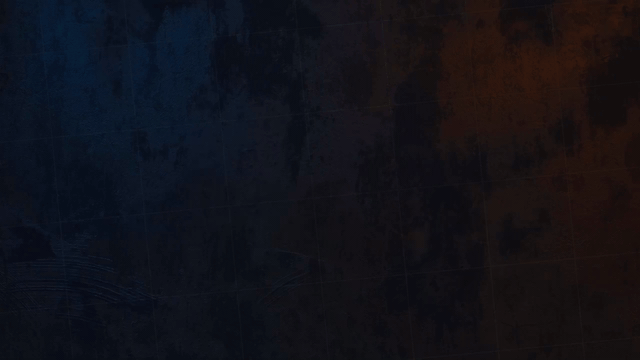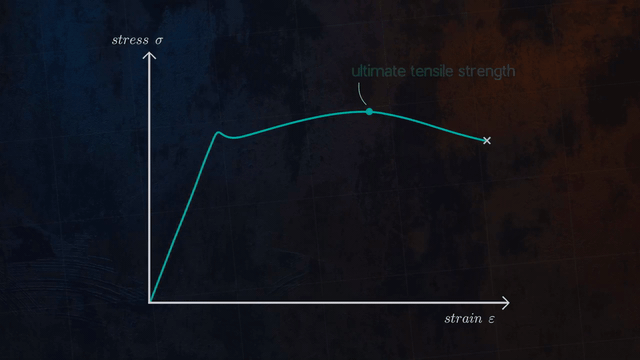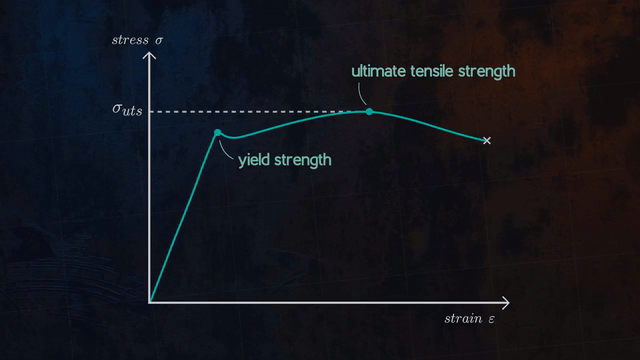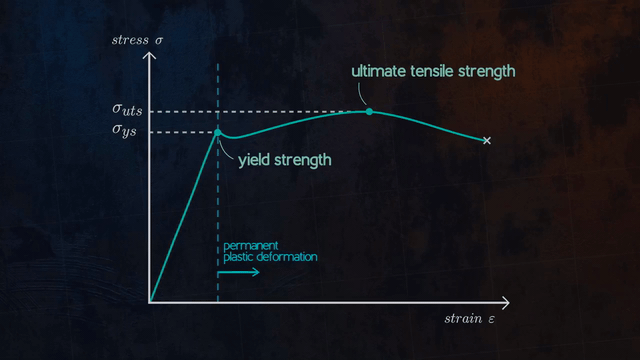Engineering Stress/Strain vs True Stress/Strain

In engineering and materials science, stress–strain curve for a material gives the relationship between stress and strain. That is obtained by gradually applying load to a test coupon and measuring the deformation from tensile testing, which the stress and strain can be determined. These curves reveal many of properties of materials, such as the Young’s modulus, the yield strength, the ultimate tensile strength and so on.

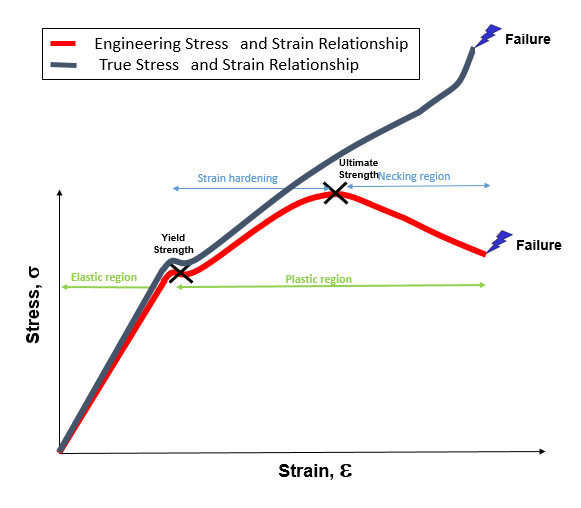
Stress/Strain graph of a tension test experiment.

Stress-strain curve for material is plotted by elongating the sample and recording the stress variation with strain until the sample fractures. The strain is set to horizontal axis and stress is set to vertical axis. It is often assumed that the cross-section area of the material does not change during the whole deformation process. This is not true since the actual area will decrease while deforming due to elastic and plastic deformation. The curve based on the original cross-section and gauge length is called the engineering stress-strain curve, while the curve based on the instantaneous cross-section area and length is called the true stress-strain curve.

For engineering stress, we assume the length and diameter of the sample remain constant throughout the whole experiment.

Engineering stress is calculated by:

{\displaystyle \sigma ={\tfrac {F}{A_{0}}}}

Engineering strain is calculated by:

{\displaystyle \varepsilon ={\tfrac {L-L_{0}}{L_{0}}}={\tfrac {\Delta L}{L_{0}}}}

True stress is the applied load divided by the actual cross-sectional area (the changing area with time) of material. Engineering stress is the applied load divided by the original cross-sectional area of material. Also known as nominal stress.

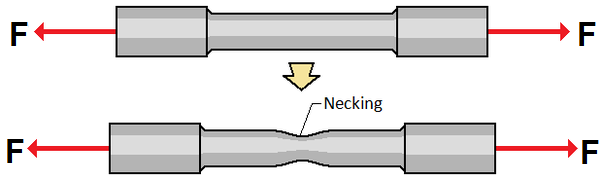
This shows the cross-section of the specimen has changed during the experiment process.

The cross-section does not remain constantly and will be different from the given value of diameter. This stress is called True Stress. Applied force is divided by the area of the section at that instant.

Before examine thoroughly true stress and strain, let’s reminisce about tensile testing (tension test).

Tensile Testing

Tensile testing, also known as tension testing, is a fundamental materials science and engineering test in which a sample is subjected to a controlled tension until failure.

Properties that are directly measured via a tensile test are ultimate tensile strength, breaking strength, maximum elongation and reduction in area. From these measurements some properties can also be determined: Young’s modulus, Poisson’s ratio, yield strength, and strain-hardening characteristics. Uniaxial tensile testing is the most commonly used for obtaining the mechanical characteristics of isotropic materials. For Some materials, biaxial tensile testing is used. The main difference between these testing machines being how load is applied on the materials.

Fracture Behaviour

Fracture behavior is considered under two main material behaviours which are called Ductile and Brittle materials.

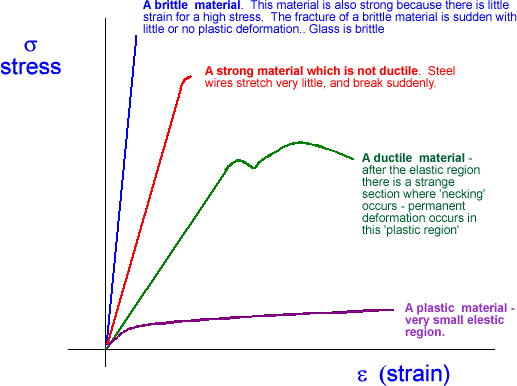
Ductile material:
Significant plastic deformation and energy absorption (toughness) reveals before fracture. Characteristic feature of ductile material is necking before material failure.

Brittle material:
Little plastic deformation or energy absorption reveals before fracture. Characteristic feature of brittle materials is different compare to ductile materials. Brittle materials fracture without any necking.

Different materials exhibit different behaviours/trends under the same loading condition.
More traditional engineering materials such as concrete under tension, glass metals and alloys exhibit adequately linear stress-strain relations until the onset of yield point.

Axial tensile test and bending test for two different materials:

A is a ductile material, and B is a brittle material.

True stress (σ_t) and true strain (ε_t) are used for accurate definition of plastic behaviour of ductile materials by considering the actual dimensions.

Brittle materials usually fracture(fail) shortly after yielding or even at yield points whereas alloys and many steels can extensively deform plastically before failure. The characteristics of each material should be chosen based on the application and design requirements.

True Stress and Strain

True stress and strain are different from engineering stress and strain.

In a tensile test, true stress is larger than engineering stress and true strain is less than engineering strain. The difference between the true and engineering stresses and strains will increase with plastic deformation. At low strains (in elastic region), the differences between the two are negligible.

True Stress (σ_t):

True stress is the stress determined by the instantaneous load acting on the instantaneous cross-sectional area.

{\displaystyle \sigma _{\text{t}}={\tfrac {F}{A}}}

True Strain (ε_t):

True strain is logarithmic and engineering strain is linear. However it appears to be almost same for small deformation owing to small values in Taylor expansion.

{\displaystyle \varepsilon _{\text{t}}=\int {\tfrac {\delta L}{L}}}

The true stress and strain can be expressed by engineering stress and strain.

For true stress:
$\sigma _{\text{t}}={\tfrac {F}{A}}={\tfrac {F}{A_{0}}}{\tfrac {A_{0}}{A}}={\tfrac {F}{A_{0}}}{\tfrac {L}{L_{0}}}=\sigma (1+\varepsilon )$

For true strain:
$\delta \varepsilon _{\text{t}}={\tfrac {\delta L}{L}}$

Integrate both sides and apply the boundary condition, $\varepsilon _{\text{t}}=\ln \left({\tfrac {L}{L_{0}}}\right)=\ln(1+\varepsilon )$

The stress and strain at the necking can be expressed as:
$\sigma _{\text{t}}={\tfrac {F}{A_{\text{neck}}}}$
$\varepsilon _{\text{t}}=\ln \left({\tfrac {A_{0}}{A_{\text{neck}}}}\right)$

In Conclusion

Engineering stress is the applied load divided by the original cross-sectional area of a material. Also known as nominal stress.
True stress is the applied load divided by the actual cross-sectional area (the changing area with respect to time) of the specimen at that load
Engineering strain is the amount that a material deforms per unit length in a tensile test. Also known as nominal strain.
True strain equals the natural log of the quotient of current length over the original length.

There is no decrease in true stress during the necking phase. Also, the results achieved from tensile and compressive tests will produce essentially the same plot when true stress and true strain are used. Engineers will produce an acceptable stress and an acceptable deformation in a given member and they want to use a diagram based on the engineering stress and the engineering strain with the cross-sectional area A₀ and the length L₀ of the member in its undeformed state.

Engineering stress: σ =F/A₀

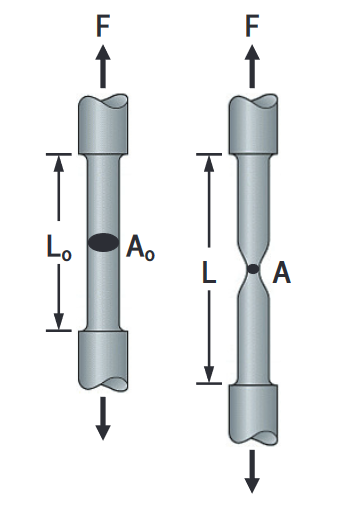
The engineering stress is obtained by dividing F by the cross-sectional area A₀ of the deformed specimen. Engineering stress becomes apparent in ductile materials after yield has started directly proportional to the force (F) decreases during the necking phase.

True stress: σ_t =F/A

The true stress (σ_t), which is proportional to F and inversely proportional to A, is observed to keep increasing until rupture of the specimen occurs.

Engineering strain: ε =δ/L₀
True strain: ε_t = ln (L/L₀)

Dividing each increment ΔL of the distance between the gage marks, by the corresponding value of L, the elementary strain is obtained:

Δε = ΔL/L₀

Adding the values of Δε
ε_t = ∑ Δε = ∑ ΔL/L
With summary by an integral, the true strain can also be expressed as:

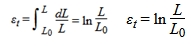
σ =F/A₀	Engineering Stress
σ_t =F/A	True Stress
ε =δ/L₀	Engineering Strain
ε_t = ln (L/L₀)	True Strain

F	Load
A₀	Cross-sectional area of specimen before deformation has taken place
A	Cross-sectional area of specimen at which the load is applied
δ	Total elongation
L₀	Original value of the gage length
L	Successive values of the length as it changes